
【題目】已知存在常數![]() ,那么函數
,那么函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數,再由函數的奇偶性可知在
上是增函數,再由函數的奇偶性可知在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
(1)判斷函數![]() 的單調性,并證明:
的單調性,并證明:
(2)將前述的函數![]() 和
和![]() 推廣為更為一般形式的函數
推廣為更為一般形式的函數![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的單調性(只須歸納出結論,不必推理證明)
的單調性(只須歸納出結論,不必推理證明)
【答案】![]() 見解析;
見解析;![]() 見解析.
見解析.
【解析】
![]() 采用換元的思想:令
采用換元的思想:令![]() 則
則![]() ;再借助復合函數單調性的判斷規則和奇偶函數在對稱區間上的單調性特點,即可得證.
;再借助復合函數單調性的判斷規則和奇偶函數在對稱區間上的單調性特點,即可得證.
![]() 由
由![]() 結論和題中
結論和題中![]() 的性質進行歸納總結,即可得出一般性結論.
的性質進行歸納總結,即可得出一般性結論.
![]() 判斷如下:
判斷如下:
![]() 在
在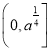 上為減函數,
上為減函數,
在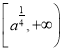 上為增函數;
上為增函數;
再由函數的奇偶性可知,
在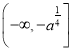 上為減函數,
上為減函數,
在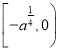 上為增函數.
上為增函數.
證明:令![]() ,
,
則![]() ,
,
由題可得,
![]() 在
在![]() 上為減函數,
上為減函數,
在![]() 上是增函數;
上是增函數;
![]() 在
在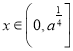 上為增函數,
上為增函數,
在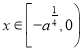 上為減函數;
上為減函數;
![]() 由復合函數單調性判斷規則知:
由復合函數單調性判斷規則知:
![]() 在
在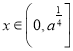 上為減函數,
上為減函數,
在 上為增函數;
上為增函數;
由題知,
![]() 為偶函數,
為偶函數,
![]() 偶函數在對稱區間上單調性相反,
偶函數在對稱區間上單調性相反,
![]()
![]() 在
在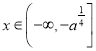 上為減函數,
上為減函數,
在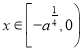 上為增函數;
上為增函數;
![]() 一般性結論:
一般性結論:
函數![]()
![]() 在
在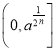 上為減函數,
上為減函數,
在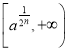 上為增函數;
上為增函數;
再由函數的奇偶性可知,
當n為奇數時,
在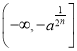 上為增函數,
上為增函數,
在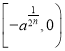 上為減函數;
上為減函數;
當n為偶數時,
在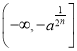 上為減函數,
上為減函數,
在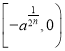 上為增函數;
上為增函數;


科目:高中數學 來源: 題型:
【題目】把三盆不同的蘭花和4盆不同的玫瑰花擺放在右圖圖案中的1,2,3,4,5,6,7所示的位置上,其中三盆蘭花不能放在一條直線上,則不同的擺放方法為( ) 
A.2680種
B.4320種
C.4920種
D.5140種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義函數F(a,b)= ![]() (a+b﹣|a﹣b|)(a,b∈R),設函數f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函數F(f(x),g(x))的最大值與零點之和為( )
(a+b﹣|a﹣b|)(a,b∈R),設函數f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函數F(f(x),g(x))的最大值與零點之和為( )
A.4
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱臺ABO﹣A1B1O1中,側面AOO1A1與側面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 
(1)證明:AB1⊥BO1;
(2)求直線AO1與平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱臺ABO﹣A1B1O1中,側面AOO1A1與側面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 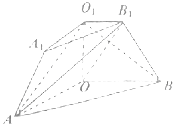
(1)證明:AB1⊥BO1;
(2)求直線AO1與平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左右焦點分別
的左右焦點分別![]()
![]() ,過
,過![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交橢圓于
交橢圓于![]() 兩點,滿足
兩點,滿足![]() .
.
(1)求橢圓![]() 的離心率.
的離心率.
(2)![]() 是橢圓
是橢圓![]() 短軸的兩個端點,設點
短軸的兩個端點,設點![]() 是橢圓
是橢圓![]() 上一點(異于橢圓
上一點(異于橢圓![]() 的頂點),直線
的頂點),直線![]() 分別與
分別與![]() 軸相交于
軸相交于![]() 兩點,
兩點,![]() 為坐標原點,若
為坐標原點,若![]() ,求橢圓
,求橢圓![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() ,下列結論中錯誤的是
,下列結論中錯誤的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函數y=f(x)的圖像是中心對稱圖形
C. 若![]() 是f(x)的極小值點,則f(x)在區間(-∞,
是f(x)的極小值點,則f(x)在區間(-∞,![]() )單調遞減
)單調遞減
D. 若![]() 是f(x)的極值點,則
是f(x)的極值點,則![]() (
(![]() )=0
)=0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com