
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
【答案】(1)![]() ;(2)
;(2)![]() 在
在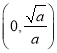 單調(diào)遞減,在
單調(diào)遞減,在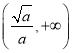 單調(diào)遞增.
單調(diào)遞增.
【解析】試題分析:(1)求導數(shù),利用導數(shù)的幾何意義曲線![]() 在點
在點![]() 處的切線斜率
處的切線斜率![]() 的值,根據(jù)點斜式可得切線方程;(2)先求出函數(shù)的導數(shù),根據(jù)
的值,根據(jù)點斜式可得切線方程;(2)先求出函數(shù)的導數(shù),根據(jù)![]() 解關于
解關于![]() 導函數(shù)的不等式可得增區(qū)間,
導函數(shù)的不等式可得增區(qū)間, ![]() 解關于
解關于![]() 的不等式,可求出函數(shù)的單調(diào)減區(qū)間.
的不等式,可求出函數(shù)的單調(diào)減區(qū)間.
試題解析:(1)當![]() 時,函數(shù)
時,函數(shù)![]() ,
, ![]() ,
,
∴![]() ,
,
∴曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(2)![]() .
.
令![]() ,解得
,解得![]() ;
;
令![]() ,解得
,解得![]() ;
;
∴![]() 在
在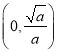 單調(diào)遞減,在
單調(diào)遞減,在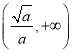 單調(diào)遞增.
單調(diào)遞增.
【方法點晴】本題主要考查利用導數(shù)求曲線切線以及及利用導數(shù)研究函數(shù)的單調(diào)性,屬于中檔題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數(shù),即
處的導數(shù),即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數(shù)不存在,切線方程為
軸平行時,在 處導數(shù)不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點
的焦點![]() 重合,且點
重合,且點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
, ![]() 與
與![]() 的公共弦長為
的公共弦長為![]() .
.
(1)求橢圓![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)若函數(shù)![]() 為定義域上的單調(diào)函數(shù),求實數(shù)
為定義域上的單調(diào)函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,函數(shù)
時,函數(shù)![]() 的兩個極值點為
的兩個極值點為![]() ,
, ![]() ,且
,且![]() .證明:
.證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】四名同學根據(jù)各自的樣本數(shù)據(jù)研究變量![]() 之間的相關關系,并求得回歸直線方程和相關系數(shù)
之間的相關關系,并求得回歸直線方程和相關系數(shù)![]() ,分別得到以下四個結論:
,分別得到以下四個結論:
①![]() ②
②![]()
③![]() ④
④![]()
其中,一定不正確的結論序號是( )
A. ②③ B. ①④ C. ①②③ D. ②③④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于函數(shù)![]() ,若在定義域內(nèi)存在實數(shù)
,若在定義域內(nèi)存在實數(shù)![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為“局部奇函數(shù)”.
為“局部奇函數(shù)”.
(1)已知二次函數(shù)![]() ,試判斷
,試判斷![]() 是否為“局部奇函數(shù)”?并說明理由;
是否為“局部奇函數(shù)”?并說明理由;
(2)若![]() 是定義在區(qū)間
是定義在區(qū)間![]() 上的“局部奇函數(shù)”,求實數(shù)
上的“局部奇函數(shù)”,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() 為定義域
為定義域![]() 上的“局部奇函數(shù)”,求實數(shù)
上的“局部奇函數(shù)”,求實數(shù)![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市英才中學的一個社會實踐調(diào)查小組,在對中學生的良好“光盤習慣”的調(diào)查中,隨機發(fā)放了120份問卷,對收回的120份有效問卷進行統(tǒng)計,得到如下![]() 列聯(lián)表:
列聯(lián)表:
做不到光盤 | 能做到光盤 | 合計 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合計 | 75 | 25 | 100 |
(1)現(xiàn)已按是否能做到光盤分層從45份女生問卷中抽取9份問卷,若從這9份問卷中隨機抽取4份,并記其中能做到光盤的問卷的份數(shù)為![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
(2)如果認為良好“光盤習慣”與性別有關犯錯誤的概率不超過![]() ,那么根據(jù)臨界值表最精確的
,那么根據(jù)臨界值表最精確的![]() 的值應為多少?請說明理由.
的值應為多少?請說明理由.
附:獨立性檢驗統(tǒng)計量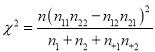 ,其中
,其中![]() .
.
獨立性檢驗臨界表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了估計某自然保護區(qū)中天鵝的數(shù)量,可以使用以下方法:先從該保護區(qū)中捕出一定數(shù)量的天鵝,例如200只,給每只天鵝做上不影響其存活的記號,然后放回保護區(qū),經(jīng)過適當?shù)臅r間,讓其和保護區(qū)中其余的天鵝充分混合,再從保護區(qū)中捕出一定數(shù)量的天鵝,例如150只,查看其中有記號的天鵝,設有20只,試根據(jù)上述數(shù)據(jù),估計該自然保護區(qū)中天鵝的數(shù)量.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,
, ![]() 為橢圓
為橢圓![]() 的右焦點,
的右焦點, ![]() ,
, ![]() .
.
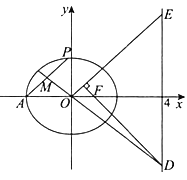
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() 為原點,
為原點, ![]() 為橢圓上一點,
為橢圓上一點, ![]() 的中點為
的中點為![]() ,直線
,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,過
,過![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為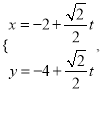 (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com