
已知函數(shù) 且
且
(Ⅰ)試用含 的代數(shù)式表示
的代數(shù)式表示 ;
;
(Ⅱ)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)令 ,設函數(shù)
,設函數(shù) 在
在 處取得極值,記點
處取得極值,記點 ,證明:線段
,證明:線段 與曲線
與曲線 存在異于
存在異于 、
、 的公共點;
的公共點;
(Ⅰ)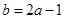 ;(Ⅱ)當
;(Ⅱ)當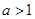 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為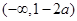 和
和 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為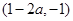 ;當
;當 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為R;當
的單調(diào)增區(qū)間為R;當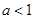 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為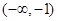 和
和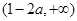 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為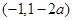
(Ⅲ)易得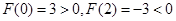 ,而
,而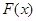 的圖像在
的圖像在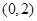 內(nèi)是一條連續(xù)不斷的曲線,
內(nèi)是一條連續(xù)不斷的曲線,
故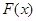 在
在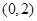 內(nèi)存在零點
內(nèi)存在零點 ,這表明線段
,這表明線段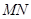 與曲線
與曲線 有異于
有異于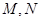 的公共點
的公共點
【解析】
試題分析:解法一:(Ⅰ)依題意,得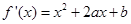
由 得
得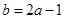
(Ⅱ)由(Ⅰ)得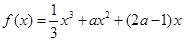
故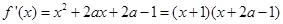
令 ,則
,則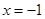 或
或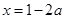
①當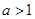 時,
時,
當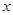 變化時,
變化時,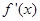 與
與 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
+ |
— |
+ |
|
|
單調(diào)遞增 |
單調(diào)遞減 |
單調(diào)遞增 |
由此得,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為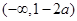 和
和 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為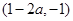
②由 時,
時,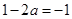 ,此時,
,此時, 恒成立,且僅在
恒成立,且僅在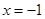 處
處 ,故函數(shù)
,故函數(shù) 的單調(diào)區(qū)間為R
的單調(diào)區(qū)間為R
③當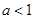 時,
時,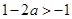 ,同理可得函數(shù)
,同理可得函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為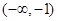 和
和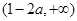 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為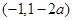
綜上:
當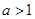 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為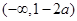 和
和 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為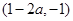 ;
;
當 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為R;
的單調(diào)增區(qū)間為R;
當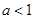 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為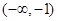 和
和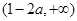 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為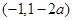
(Ⅲ)當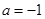 時,得
時,得
由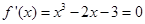 ,得
,得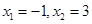
由(Ⅱ)得 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為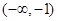 和
和 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為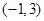
所以函數(shù) 在
在 處取得極值。
處取得極值。
故
所以直線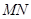 的方程為
的方程為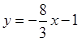
由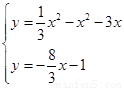 得
得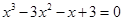
令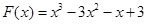
易得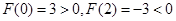 ,而
,而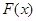 的圖像在
的圖像在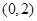 內(nèi)是一條連續(xù)不斷的曲線,
內(nèi)是一條連續(xù)不斷的曲線,
故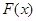 在
在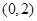 內(nèi)存在零點
內(nèi)存在零點 ,這表明線段
,這表明線段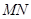 與曲線
與曲線 有異于
有異于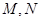 的公共點
的公共點
解法二:
(Ⅲ)當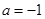 時,得
時,得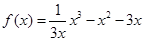 ,由
,由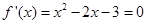 ,得
,得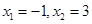
由(Ⅱ)得 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為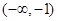 和
和 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為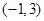 ,所以函數(shù)
,所以函數(shù) 在
在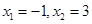 處取得極值,
處取得極值,
故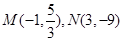
所以直線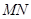 的方程為
的方程為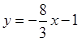
由 得
得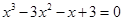
解得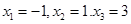
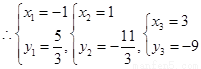
所以線段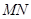 與曲線
與曲線 有異于
有異于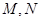 的公共點
的公共點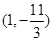 。
。
考點:本題考查了導數(shù)的運用
點評:本題是在知識的交匯點處命題,將函數(shù)、導數(shù)、不等式、方程的知識融合在一起進行考查,重點考查了利用導數(shù)研究函數(shù)的極值與最值等知識.導數(shù)題目是高考的必考題,且常考常新,但是無論如何少不了對基礎知識的考查,因此備考中要強化基礎題的訓練.


科目:高中數(shù)學 來源: 題型:
(07年福建卷理)(本小題滿分14分)已知函數(shù)![]()
(Ⅰ)若![]() ,試確定函數(shù)
,試確定函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() ,且對于任意
,且對于任意![]() ,
,![]() 恒成立,試確定實數(shù)
恒成立,試確定實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)設函數(shù)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本小題滿分15分)已知函數(shù)![]()
![]() 且
且![]() .
.
(Ⅰ)試用含![]() 式子表示
式子表示![]() ;(Ⅱ)求
;(Ⅱ)求![]() 的單調(diào)區(qū)間;(Ⅲ)若
的單調(diào)區(qū)間;(Ⅲ)若![]() ,試求
,試求![]() 在區(qū)間
在區(qū)間![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年山東省高三第二次(3月)周測理科數(shù)學試卷(解析版) 題型:解答題
已知函數(shù)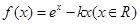
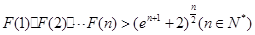 .
.
(Ⅰ)若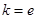 ,試確定函數(shù)
,試確定函數(shù)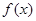 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若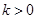 且對任意
且對任意 恒成立,試確定實數(shù)
恒成立,試確定實數(shù)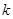 的取值范圍;
的取值范圍;
(Ⅲ)設函數(shù) ,求證:
,求證: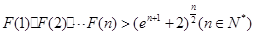 .
.
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆河北省高二下學期第二次月考理科數(shù)學試卷(解析版) 題型:解答題
已知函數(shù)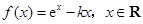
(Ⅰ)若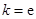 ,試確定函數(shù)
,試確定函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若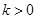 ,且對于任意
,且對于任意 ,
, 恒成立,試確定實數(shù)
恒成立,試確定實數(shù)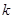 的取值范圍;
的取值范圍;
(Ⅲ)設函數(shù)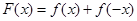 ,求證:
,求證: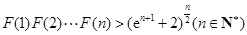 .
.
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆內(nèi)蒙古巴彥淖爾市中學高二下期中文科數(shù)學試卷(解析版) 題型:解答題
已知函數(shù)f(x)=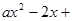 1 .
1 .
(1)試討論函數(shù)f(x)的單調(diào)性;
(2)若 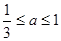 ,且f(x)在區(qū)間[1,3]上的最大值為M(a) ,最小值為N(a),
,且f(x)在區(qū)間[1,3]上的最大值為M(a) ,最小值為N(a),
令g(a)= M(a)-N(a),求 g(a)的表達式,試求g(a)的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com