
【題目】[選修4一4:坐標系與參數方程]已知直線l過原點且傾斜角為![]() ,
, ![]()
![]()
![]() ,以原點O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C 的極坐標方程為psin
,以原點O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C 的極坐標方程為psin![]()
![]() =4cos
=4cos![]() .
.
(I)寫出直線l的極坐標方程和曲線C 的直角坐標方程;
(Ⅱ)已知直線l過原點且與直線l相互垂直,若l![]() C=-M,l
C=-M,l![]() C=N,其中M,N不與原點重合,求△OMN 面積的最小值.
C=N,其中M,N不與原點重合,求△OMN 面積的最小值.
【答案】(1)![]() =
=![]() ,y
,y![]() =4x.(2)16
=4x.(2)16
【解析】試題分析:(1)根據極角定義得直線l的極坐標方程,根據![]() 將曲線C 的極坐標方程化為直角坐標方程;(2)先確定直線
將曲線C 的極坐標方程化為直角坐標方程;(2)先確定直線![]() 極坐標方程,代入求得
極坐標方程,代入求得![]() ,根據面積公式可得S,最后根據三角函數有界性求最小值.
,根據面積公式可得S,最后根據三角函數有界性求最小值.
試題解析:解:(I)依題意,直線l的極坐標方程為![]() =
=![]() (
(![]() ≠
≠![]() ,
, ![]() ∈R)
∈R)
曲線C: ![]() Sin
Sin![]()
![]() =4cos
=4cos![]() ,
,![]() sin
sin ![]() =4
=4![]() cos
cos![]() ,直角坐標方程為y
,直角坐標方程為y![]() =4x.
=4x.
(Ⅱ)把θ=![]() 代入
代入![]() sin
sin ![]() =4cos
=4cos![]() ,得
,得![]() =
=![]() .
.
可知直線l的極坐標方程為![]() =
=![]() +
+![]() (
(![]() ∈R)
∈R)
代入![]() sin
sin![]()
![]() =4cos
=4cos![]() ,得
,得![]() cos
cos ![]() =-4sin
=-4sin![]() ,所以
,所以![]() =-
=-![]() ,
,
S△![]() =
=![]() |OM|·|ON|=2|
|OM|·|ON|=2|![]() |·|
|·|![]() |=
|=![]() ≥16,(當且僅當
≥16,(當且僅當![]() =
=![]() 時,取“=”)
時,取“=”)
即△OMN面積的最小值為16.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,一條準線方程為
,一條準線方程為![]() 過橢圓的上頂點A作一條與x軸、y軸都不垂直的直線交橢圓于另一點P,P關于x軸的對稱點為Q.
過橢圓的上頂點A作一條與x軸、y軸都不垂直的直線交橢圓于另一點P,P關于x軸的對稱點為Q.
![]() 求橢圓的方程;
求橢圓的方程;
![]() 若直線AP,AQ與x軸交點的橫坐標分別為m,n,求證:mn為常數,并求出此常數.
若直線AP,AQ與x軸交點的橫坐標分別為m,n,求證:mn為常數,并求出此常數.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國慶70周年慶典磅礴而又歡快的場景,仍歷歷在目.已知慶典中某省的游行花車需要用到某類花卉,而該類花卉有甲、乙兩個品種,花車的設計團隊對這兩個品種進行了檢測.現從兩個品種中各抽測了10株的高度,得到如下莖葉圖.下列描述正確的是( )

A.甲品種的平均高度大于乙品種的平均高度,且甲品種比乙品種長的整齊
B.甲品種的平均高度大于乙品種的平均高度,但乙品種比甲品種長的整齊
C.乙品種的平均高度大于甲品種的平均高度,且乙品種比甲品種長的整齊
D.乙品種的平均高度大于甲品種的平均高度,但甲品種比乙品種長的整齊
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x(e![]() +1)
+1)
(I)求函數y=f(x)的圖象在點(0,f(0))處的切線方程;
(II)若函數g(x)=f(x)-ae![]() -x,求函數g(x)在[1,2]上的最大值。
-x,求函數g(x)在[1,2]上的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為緩減人口老年化帶來的問題,中國政府在2016年1月1日作出全國統(tǒng)一實施全面的“二孩”政策,生“二孩”是目前中國比較流行的元素![]() 某調查機構對某校學生做了一個是否同意父母生“二孩”抽樣調查,該調查機構從該校隨機抽查了100名不同性別的學生,調查統(tǒng)計他們是同意父母生“二孩”還是反對父母生“二孩”
某調查機構對某校學生做了一個是否同意父母生“二孩”抽樣調查,該調查機構從該校隨機抽查了100名不同性別的學生,調查統(tǒng)計他們是同意父母生“二孩”還是反對父母生“二孩”![]() 現已得知100人中同意父母生“二孩”占
現已得知100人中同意父母生“二孩”占![]() ,統(tǒng)計情況如表:
,統(tǒng)計情況如表:
性別屬性 | 同意父母生“二孩” | 反對父母生“二孩” | 合計 |
男生 | 10 | ||
女生 | 30 | ||
合計 | 100 |
![]() 請補充完整上述列聯表;
請補充完整上述列聯表;
![]() 根據以上資料你是否有
根據以上資料你是否有![]() 把握,認為是否同意父母生“二孩”與性別有關?請說明理由.
把握,認為是否同意父母生“二孩”與性別有關?請說明理由.
參考公式與數據:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某公司生產的商品A每件售價為5元時,年銷售10萬件,
(1)據市場調查,若價格每提高一元,銷量相應減少1萬件,要使銷售收入不低于原銷售收入,該商品的銷售價格最多提高多少元?
(2)為了擴大該商品的影響力,公司決定對該商品的生產進行技術革新,將技術革新后生產的商品售價提高到每件![]() 元,公司擬投入
元,公司擬投入![]() 萬元作為技改費用,投入
萬元作為技改費用,投入![]() 萬元作為宣傳費用。試問:技術革新后生產的該商品銷售量m至少應達到多少萬件時,才可能使技術革新后的該商品銷售收入等于原銷售收入與總投入之和?
萬元作為宣傳費用。試問:技術革新后生產的該商品銷售量m至少應達到多少萬件時,才可能使技術革新后的該商品銷售收入等于原銷售收入與總投入之和?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是首項為a,公差為d的等差數列(d≠0),
是首項為a,公差為d的等差數列(d≠0), ![]() 是其前n項的和.記
是其前n項的和.記![]() ,n∈N*,其中c為實數.
,n∈N*,其中c為實數.
(1)若c=0,且b1,b2,b4成等比數列,證明:Snk=n2Sk(k,n∈N*);
(2)若{![]() }是等差數列,證明:c=0.
}是等差數列,證明:c=0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機和電子閱讀器越來越普及,人們的閱讀習慣也發(fā)生了改變,手機和電子閱讀產品方便易攜帶,越來越多的人習慣通過手機或電子閱讀器閱讀.某電子書閱讀器廠商隨機調查了![]() 人,統(tǒng)計了這
人,統(tǒng)計了這![]() 人每日平均通過手機或電子閱讀器閱讀的時間(單位:分鐘),由統(tǒng)計數據得到如下頻率分布直方圖,已知閱讀時間在
人每日平均通過手機或電子閱讀器閱讀的時間(單位:分鐘),由統(tǒng)計數據得到如下頻率分布直方圖,已知閱讀時間在![]() ,
, ![]() ,
, ![]() 三組對應的人數依次成等差數列.
三組對應的人數依次成等差數列.
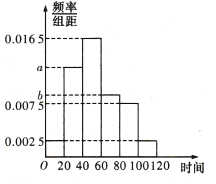
(1)求頻率分布直方圖中![]() ,
, ![]() 的值;
的值;
(2)若將日平均閱讀時間不少于![]() 分鐘的用戶定義為“電子閱讀發(fā)燒友”,將日平均閱讀時間少于
分鐘的用戶定義為“電子閱讀發(fā)燒友”,將日平均閱讀時間少于![]() 分鐘的用戶定義為“電子閱讀潛在愛好者”,現從上述“電子閱讀發(fā)燒友”與“電子閱讀潛在愛好者”的人中按分層抽樣選出
分鐘的用戶定義為“電子閱讀潛在愛好者”,現從上述“電子閱讀發(fā)燒友”與“電子閱讀潛在愛好者”的人中按分層抽樣選出![]() 人,再從這
人,再從這![]() 人中任取
人中任取![]() 人,求恰有
人,求恰有![]() 人為“電子閱讀發(fā)燒友”的概率.
人為“電子閱讀發(fā)燒友”的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com