
【題目】已知點A(a,3),圓C:(x﹣1)2+(y﹣2)2=4.
(1)設a=4,求過點A且與圓C相切的直線方程;
(2)設a=3,直線l過點A且被圓C截得的弦長為![]() ,求直線l的方程.
,求直線l的方程.
科目:高中數學 來源: 題型:
【題目】己知p:函數f(x)在R上是增函數,f(m2)<f(m+2)成立;q:方程![]() 1(m∈R)表示雙曲線.
1(m∈R)表示雙曲線.
(1)若p為真命題,求m的取值范圍;
(2)若p∨q為真,p∧q為假,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方形![]() 的邊長為
的邊長為![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起,使平面
折起,使平面![]() 平面
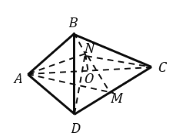
平面![]() ,得到如圖所示的三棱錐
,得到如圖所示的三棱錐![]() ,若
,若![]() 為
為![]() 邊的中點,
邊的中點,![]() 分別為
分別為![]() 上的動點(不包括端點),且
上的動點(不包括端點),且![]() ,設
,設![]() ,則三棱錐
,則三棱錐![]() 的體積取得最大值時,三棱錐
的體積取得最大值時,三棱錐![]() 的內切球的半徑為_______.
的內切球的半徑為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設各項均為正數的數列{an}的前n項和為Sn,滿足:對任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求數列{an}的通項公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為0的等差數列{an},其前n項和為Sn,若S10=100,a1,a2,a5成等比數列.
(1)求{an}的通項公式;
(2)bn=anan+1+an+an+1+1,求數列![]() 的前n項和Tn.
的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
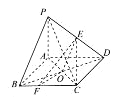
【題目】如圖所示,底面為正方形的四棱錐P-ABCD中,AB=2,PA=4,PB=PD=![]() ,AC與BD相交于點O,E為PD中點.
,AC與BD相交于點O,E為PD中點.
(1)求證:EO//平面PBC;
(2)設線段BC上點F滿足CF=2BF,求銳二面角E-OF-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com