
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,點E為線段PC的中點,點F在線段AB上.
,∠PDC=120°,點E為線段PC的中點,點F在線段AB上. 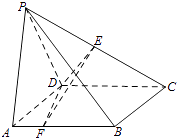
(1)若AF= ![]() ,求證:CD⊥EF;
,求證:CD⊥EF;
(2)設平面DEF與平面DPA所成二面角的平面角為θ,試確定點F的位置,使得cosθ= ![]() .
.
【答案】
(1)證明:在△PCD中,PD=CD=2,
∵E為PC的中點,∴DE平分∠PDC,∠PDE=60°,
∴在Rt△PDE中,DE=PDcos60°=1,
過E作EH⊥CD于H,則 ![]() ,連結FH,
,連結FH,

∵ ![]() ,∴四邊形AFHD是矩形,
,∴四邊形AFHD是矩形,
∴CD⊥FH,又CD⊥EH,FH∩EH=H,∴CD⊥平面EFH,
又EF平面EFH,∴CD⊥EF.
(2)解:∵AD=PD=2, ![]() ,∴AD⊥PD,又AD⊥DC,
,∴AD⊥PD,又AD⊥DC,
∴AD⊥平面PCD,
又AD平面ABCD,∴平面PCD⊥平面ABCD.
過D作DG⊥DC交PC于點G,則由平面PCD⊥平面ABCD知,DG⊥平面ABCD,
故DA,DC,DG兩兩垂直,以D為原點,以DA,DC,DG所在直線分別為x,y,z軸,
建立如圖所示空間直角坐標系O﹣xyz,
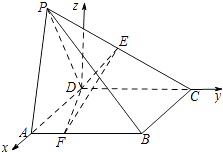
則A(2,0,0),B(2,2,0),C(0,2,0), ![]() ,
,
又知E為PC的中點,E ![]() ,設F(2,t,0),
,設F(2,t,0),
則 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
設平面DEF的法向量為 ![]() =(x1,y1,z1),
=(x1,y1,z1),
則  ,∴
,∴  ,
,
取z1=﹣2,得平面DEF的一個法向量 ![]() ,
,
設平面ADP的法向量為 ![]() =(x2,y2,z2),
=(x2,y2,z2),
則 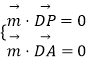 ,∴
,∴ ![]() ,
,
取z2=1,得 ![]() .
.
∴ ![]() ,解得
,解得 ![]() ,
,
∴當 ![]() 時,滿足
時,滿足 ![]() .
.
【解析】(1)過E作EH⊥CD于H,連結FH,推導出四邊形AFHD是矩形,由此能證明CD⊥F.(2)過D作DG⊥DC交PC于點G,以D為原點,以DA,DC,DG所在直線分別為x,y,z軸,建立空間直角坐標系O﹣xyz,利用向量法能求出當 ![]() 時,滿足
時,滿足 ![]() .
.
【考點精析】解答此題的關鍵在于理解空間中直線與直線之間的位置關系的相關知識,掌握相交直線:同一平面內,有且只有一個公共點;平行直線:同一平面內,沒有公共點;異面直線: 不同在任何一個平面內,沒有公共點.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知正三角形ABC的邊長為2,D、E、F分別是BC、CA、AB的中點.
(1)在三角形內部隨機取一點P,求滿足|PB|≥1且|PC|≥1的概率;
(2)在A、B、C、D、E、F這6點中任選3點,記這3點圍成圖形的面積為ξ,求隨機變量ξ的分布列與數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 為等比數列,
為等比數列,![]() ,公比為
,公比為![]() ,且
,且![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和.
項和.
(1)若![]() ,求
,求![]() ;
;
(2)若調換![]() 的順序后能構成一個等差數列,求
的順序后能構成一個等差數列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常數![]() ,使得對任意正整數
,使得對任意正整數![]() ,不等式
,不等式![]() 總成立?若存在,求出
總成立?若存在,求出![]() 的范圍,若不存在,請說明理由.
的范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,P為雙曲線 ![]() ﹣y2=1(a>0)上一點,過P作兩條漸近線的平行線交點分別為A,B,若平行四邊形OAPB的面積為
﹣y2=1(a>0)上一點,過P作兩條漸近線的平行線交點分別為A,B,若平行四邊形OAPB的面積為 ![]() ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )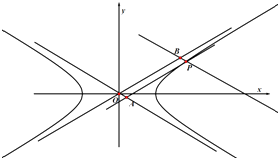
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +y2=1與直線l:y=kx+m相交于E、F兩不同點,且直線l與圓O:x2+y2=
+y2=1與直線l:y=kx+m相交于E、F兩不同點,且直線l與圓O:x2+y2= ![]() 相切于點W(O為坐標原點).
相切于點W(O為坐標原點).
(1)證明:OE⊥OF;
(2)設λ= ![]() ,求實數λ的取值范圍.
,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列![]() 的前
的前![]() 項和為
項和為![]() ,在同一個坐標系中,
,在同一個坐標系中,![]() 及
及![]() 的部分圖象如圖所示,則( ).
的部分圖象如圖所示,則( ).

A. 當![]() 時,
時,![]() 取得最大值 B. 當
取得最大值 B. 當![]() 時,
時,![]() 取得最大值
取得最大值
C. 當![]() 時,
時,![]() 取得最小值 D. 當
取得最小值 D. 當![]() 時,
時,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2+ax+b,a,b∈R.
(1)若2a+b=4,證明:|f(x)|在區間[0,4]上的最大值M(a)≥12;
(2)存在實數a,使得當x∈[0,b]時,1≤f(x)≤10恒成立,求實數b的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB為直徑的圓,DC的延長線與AB的延長線交于點E.
(Ⅰ)求證:DC是⊙O的切線;
(Ⅱ)若EB=6,EC=6 ![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com