
【題目】已知函數![]() ,其中
,其中![]() ,e為自然對數的底數.
,e為自然對數的底數.
(1)當![]() 時,求
時,求![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)求函數![]() 的單調區間;
的單調區間;
(3)若存在![]() (
(![]() ),使得
),使得![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 的遞增區間是
的遞增區間是![]() ,無遞減區間;當
,無遞減區間;當![]() 時,
時,![]() 的遞增區間是
的遞增區間是![]() 和
和![]() ,遞減區間是
,遞減區間是![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)對![]() 求導,可得
求導,可得![]() 與
與![]() 的值,可得
的值,可得![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)令![]() ,可得
,可得![]() ,對其分
,對其分![]() ,
,![]() 進行討論,可得
進行討論,可得![]() 的取值范圍及
的取值范圍及![]() 的單調區間;
的單調區間;
(3)由(2)知,![]() ,且
,且![]() ,可得
,可得![]() 關于
關于![]() 的函數,對其求導可得其單調性,可得證明.
的函數,對其求導可得其單調性,可得證明.
解:因為![]() 時,
時,![]() 對
對![]() 恒成立,
恒成立,
所以![]() 定義域為
定義域為![]() ,且
,且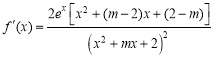 ,
,
(1)當![]() 時,
時,![]() ,
,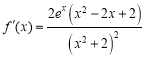 ,所以
,所以![]() ,
,
所以![]() 在
在![]() 處的切線方程為:
處的切線方程為:![]() .
.
(2)令![]() 得,
得,![]() , (※)
, (※)
①當![]() ,即
,即![]() 時,又
時,又![]() ,
,
所以![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增;
上單調遞增;
②當![]() ,解得
,解得![]() 或
或![]() ,又
,又![]() ,所以
,所以![]() 時,
時,
由方程(※)解得,![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 的遞增區間是
的遞增區間是![]() ;
;
當![]() 時,
時,![]() ,
,![]() 的遞減區間是
的遞減區間是![]() .
.
綜上,當![]() 時,
時,![]() 的遞增區間是
的遞增區間是![]() ,無遞減區間;
,無遞減區間;
當![]() 時,
時,![]() 的遞增區間是
的遞增區間是![]() 和
和![]() ,遞減區間是
,遞減區間是![]() .
.
(3)由(2)知,![]() ,且
,且![]() ,
,
所以![]() ,
,
因為![]() ,
,![]() ,代入上式得
,代入上式得
![]()
![]()
![]()
![]() ,
,
令![]() ,
,![]() ,
,
則![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,即證得
,即證得![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,焦點為
,焦點為![]() 的拋物線
的拋物線![]() 的準線被橢圓
的準線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若點![]() 、
、![]() 到直線
到直線![]() 的距離之積為
的距離之積為![]() ,求證:直線
,求證:直線![]() 與橢圓
與橢圓![]() 相切.
相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() ,
,![]() 為任意實數.
為任意實數.
(1)求證:直線![]() 必與圓
必與圓![]() 相交;
相交;
(2)![]() 為何值時,直線
為何值時,直線![]() 被圓
被圓![]() 截得的弦長
截得的弦長![]() 最短?最短弦長是多少?
最短?最短弦長是多少?
(3)若直線![]() 被圓
被圓![]() 截得的弦
截得的弦![]() 的中點為點
的中點為點![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現定義:設![]() 是非零實常數,若對于任意的
是非零實常數,若對于任意的![]() ,都有
,都有![]() ,則稱函數
,則稱函數![]() 為“關于的
為“關于的![]() 偶型函數”
偶型函數”
(1)請以三角函數為例,寫出一個“關于2的偶型函數”的解析式,并給予證明
(2)設定義域為的“關于的![]() 偶型函數”在區間
偶型函數”在區間![]() 上單調遞增,求證在區間
上單調遞增,求證在區間![]() 上單調遞減
上單調遞減
(3)設定義域為![]() 的“關于
的“關于![]() 的偶型函數”
的偶型函數”![]() 是奇函數,若
是奇函數,若![]() ,請猜測
,請猜測![]() 的值,并用數學歸納法證明你的結論
的值,并用數學歸納法證明你的結論
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生對函數![]() 的性質進行研究,得出如下的結論:
的性質進行研究,得出如下的結論:
![]() 函數在
函數在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
![]() 點
點![]() 是函數圖象的一個對稱中心;
是函數圖象的一個對稱中心;
![]() 函數圖象關于直線
函數圖象關于直線![]() 對稱;
對稱;
![]() 存在常數
存在常數![]() ,使
,使![]() 對一切實數x均成立,
對一切實數x均成立,
其中正確命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
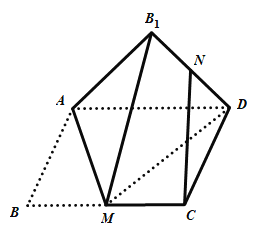
【題目】如圖,矩形![]() 中,
中,![]() 為
為![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,連結
,連結![]() ,
,![]() 為
為![]() 的中點,則在翻折過程中,下列說法中所有正確的是( )
的中點,則在翻折過程中,下列說法中所有正確的是( )
A.存在某個位置,使得![]()
B.翻折過程中,![]() 的長是定值
的長是定值
C.若![]() ,則
,則![]()
D.若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,三棱錐
的體積最大時,三棱錐![]() 的外接球的表面積是
的外接球的表面積是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新中國成立70周年以來,黨中央國務院高度重視改善人民生活,始終把提高人民生活水平作為一切工作的出發點和落腳點城鄉居民收入大幅增長,居民生活發生了翻天覆地的變化.下面是1949年及2015年~2018年中國居民人均可支配收入(元)統計圖.以下結論中不正確的是( )
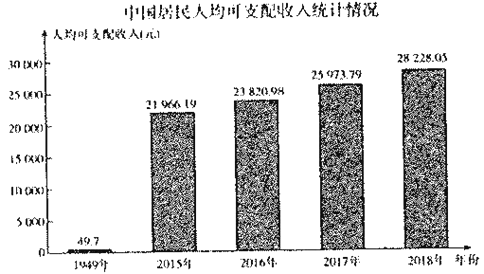
A.20l5年-2018年中國居民人均可支配收入與年份成正相關
B.2018年中居民人均可支配收入超過了1949年的500倍
C.2015年-2018年中國居民人均可支配收入平均超過了24000元
D.2015年-2018年中圍居民人均可支配收入都超過了1949年的500倍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com