
【題目】已知函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 的單調區間;
的單調區間;
(2)若函數![]() 在區間
在區間![]() 上不單調,求實數
上不單調,求實數![]() 的取值范圍;
的取值范圍;
(3)求證:![]() 或
或![]() 是函數
是函數![]() 在
在![]() 上有三個不同零點的必要不充分條件.
上有三個不同零點的必要不充分條件.
【答案】(1)函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,沒有單調遞減區間. (2)
,沒有單調遞減區間. (2)![]() (3)見解析
(3)見解析
【解析】
(1)將參數值k代入解析式,對函數求導,得到導函數大于0,進而得到函數只有增區間沒有減區間;(2)對函數求導,![]() 在區間
在區間![]() 上不單調所以
上不單調所以![]() 在
在![]() 上有實數解,且無重根,變量分離即方程
上有實數解,且無重根,變量分離即方程![]() 有解,通過換元得到新函數的單調性,對方程的根進行討論即可;(3)證明:
有解,通過換元得到新函數的單調性,對方程的根進行討論即可;(3)證明:![]() 或
或![]() 則函數
則函數![]() 在
在![]() 上不能有三個不同零點,證明,函數有3個不同零點則
上不能有三個不同零點,證明,函數有3個不同零點則![]() 或
或![]() 即可.
即可.
(1)若k=-1,則![]() ,所以
,所以![]()
由于△=16-48<0,
![]()
所以函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,沒有單調遞減區間.
,沒有單調遞減區間.
(2)因![]()
![]() ,因
,因![]() 在區間
在區間![]() 上不單調,
上不單調,
所以![]() 在
在![]() 上有實數解,且無重根,
上有實數解,且無重根,
由![]() 得
得![]()
![]()
令![]() 有
有![]() ,記
,記![]() 則
則![]() ,
,
所以在![]()
![]() 上,h(t)單調遞減,在
上,h(t)單調遞減,在![]()
![]() 上, h(t)單調遞增,
上, h(t)單調遞增,
所以有![]() ,于是得
,于是得![]()
而當![]() 時有
時有![]() 在
在![]() 上有兩個相等的實根
上有兩個相等的實根![]() ,故舍去
,故舍去
所以![]() .
.
(3)因為![]()
所以,當△=![]() ,即
,即![]() 時
時
函數![]() 在R上單調遞增
在R上單調遞增
故![]() 在R上不可能有三個不同零點
在R上不可能有三個不同零點
所以,若![]() 在R上有三個不同零點,則必有△
在R上有三個不同零點,則必有△![]() ,
,
即![]() 是
是![]() 在R上有三個不同零點的必要條件.
在R上有三個不同零點的必要條件.
而當![]() ,
,![]() 時,滿足
時,滿足![]()
但![]()
即此時![]() 只有兩個不同零點
只有兩個不同零點
同樣,當![]() 時,滿足
時,滿足![]() ,
,
但![]()
即此時![]() 也只有兩個不同零點
也只有兩個不同零點
故k<-2或k>7是![]() 在R上有三個不同零點的必要不充分條件.
在R上有三個不同零點的必要不充分條件.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】為了解共享單車在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了![]() 人進行分析,得到如下列聯表(單位:人).
人進行分析,得到如下列聯表(單位:人).
經常使用 | 偶爾使用或不使用 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
(1)根據以上數據,能否在犯錯誤的概率不超過![]() 的前提下認為
的前提下認為![]() 市使用共享單車的情況與年齡有關;
市使用共享單車的情況與年齡有關;
(2)(i)現從所選取的![]() 歲以上的網友中,采用分層抽樣的方法選取
歲以上的網友中,采用分層抽樣的方法選取![]() 人,再從這
人,再從這![]() 人中隨機選出
人中隨機選出![]() 人贈送優惠券,求選出的
人贈送優惠券,求選出的![]() 人中至少有
人中至少有![]() 人經常使用共享單車的概率;
人經常使用共享單車的概率;
(ii)將頻率視為概率,從![]() 市所有參與調查的網友中隨機選取
市所有參與調查的網友中隨機選取![]() 人贈送禮品,記其中經常使用共享單車的人數為
人贈送禮品,記其中經常使用共享單車的人數為![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
參考公式: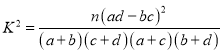 ,其中
,其中![]() .
.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).在以坐標原點
為參數).在以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,且與直角坐標系長度單位相同的極坐標系中,曲線
軸的正半軸為極軸,且與直角坐標系長度單位相同的極坐標系中,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() .若直
.若直![]() 與曲線
與曲線![]() 相交于兩點
相交于兩點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了積極支持雄安新區建設,某投資公司計劃明年投資1000萬元給雄安新區甲、乙兩家科技企業,以支持其創新研發計劃,經有關部門測算,若不受中美貿易戰影響的話,每投入100萬元資金,在甲企業可獲利150萬元,若遭受貿易戰影響的話,則將損失50萬元;同樣的情況,在乙企業可獲利100萬元,否則將損失20萬元,假設甲、乙兩企業遭受貿易戰影響的概率分別為0.6和0.5.
(1)若在甲、乙兩企業分別投資500萬元,求獲利1250萬元的概率;
(2)若在兩企業的投資額相差不超過300萬元,求該投資公司明年獲利約在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是一個“數陣”:
1 | ( ) | ( ) | ( ) | … |
| … |
( ) | 1 | ( ) | ( ) | … |
| … |
( ) | ( ) | ( ) | 1 | … |
| … |
… | … | … | … | … | … | … |
|
|
|
| … |
| … |
… | … | … | … | … | … | … |
其中每行都是公差不為0等差數列,每列都是等比數列,![]() 表示位于第i行第j列的數.
表示位于第i行第j列的數.
(1)寫出![]() 的值:
的值:
(2)寫出![]() 的計算公式,以及第2020個1所在“數陣”中所在的位置.
的計算公式,以及第2020個1所在“數陣”中所在的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,橢圓
,橢圓![]() :
:![]() 與雙曲線
與雙曲線![]() :
:![]() 的焦點相同.
的焦點相同.
(1)求橢圓![]() 與雙曲線
與雙曲線![]() 的方程;
的方程;
(2)過雙曲線![]() 的右頂點作兩條斜率分別為
的右頂點作兩條斜率分別為![]() ,
,![]() 的直線
的直線![]() ,
,![]() ,分別交雙曲線
,分別交雙曲線![]() 于點
于點![]() ,
,![]() (
(![]() ,
,![]() 不同于右頂點),若
不同于右頂點),若![]() ,求證:直線
,求證:直線![]() 的傾斜角為定值,并求出此定值;
的傾斜角為定值,并求出此定值;
(3)設點![]() ,若對于直線
,若對于直線![]() ,橢圓
,橢圓![]() 上總存在不同的兩點
上總存在不同的兩點![]() 與
與![]() 關于直線
關于直線![]() 對稱,且
對稱,且![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有以下說法:
①一年按365天計算,兩名學生的生日相同的概率是![]() ;②買彩票中獎的概率為0.001,那么買1 000張彩票就一定能中獎;③乒乓球賽前,決定誰先發球,抽簽方法是從1~10共10個數字中各抽取1個,再比較大小,這種抽簽方法是公平的;④昨天沒有下雨,則說明“昨天氣象局的天氣預報降水概率是90%”是錯誤的.
;②買彩票中獎的概率為0.001,那么買1 000張彩票就一定能中獎;③乒乓球賽前,決定誰先發球,抽簽方法是從1~10共10個數字中各抽取1個,再比較大小,這種抽簽方法是公平的;④昨天沒有下雨,則說明“昨天氣象局的天氣預報降水概率是90%”是錯誤的.
根據我們所學的概率知識,其中說法正確的序號是___.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)用分段函數的形式表示函數f(x);
(2)在平面直角坐標系中畫出函數f(x)的圖象;

(3)在同一平面直角坐標系中,再畫出函數g(x)=![]() (x>0)的圖象(不用列表),觀察圖象直接寫出當x>0時,不等式f(x)>
(x>0)的圖象(不用列表),觀察圖象直接寫出當x>0時,不等式f(x)> ![]() 的解集.
的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com