
【題目】設函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)![]() ,
,![]() 恒成立,求最大的正整數
恒成立,求最大的正整數![]() 的值;
的值;
(3)![]() ,
,![]() 且
且![]() ,證明:
,證明:![]() .
.
【答案】(1)單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]() ;(2)8;(3)證明見解析.
;(2)8;(3)證明見解析.
【解析】
(1)![]() 時,函數
時,函數![]() ,求導可得
,求導可得![]() ,可知函數
,可知函數![]() 在
在![]() 上單調遞增,而
上單調遞增,而![]() ,即可得出單調區間;
,即可得出單調區間;
(2)![]() ,
,![]() 恒成立,即
恒成立,即![]() ,化為
,化為![]() 很成立,利用導數研究函數的單調性求得
很成立,利用導數研究函數的單調性求得![]() 的最小值即可求解.
的最小值即可求解.
(3)![]() ,
,![]() 且
且![]() ,要證明:
,要證明:![]() .
.
![]() ,
,![]() ,
,
即![]() ,
,
令![]() ,即證明
,即證明![]() 時,
時,![]() 恒成立;
恒成立;![]() 時,
時,![]() 恒成立,利用導數研究
恒成立,利用導數研究![]() 單調性,進而證明即可.
單調性,進而證明即可.
(1)解:![]() 時,函數
時,函數![]() ,
,
則![]() ,
,
因為函數![]() 在
在![]() 上單調遞增,
上單調遞增,
且![]() ,∴
,∴![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,
,
∴函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]() .
.
(2)解:因為![]() ,
,![]() 恒成立,
恒成立,
即![]() 恒成立,則
恒成立,則![]() 恒成立.
恒成立.
因為![]() ,
,
令![]() ,所以
,所以![]() ,則當
,則當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以當![]() 時,函數
時,函數![]() 取得極小值即最小值,
取得極小值即最小值,
因為![]() ,
,
所以![]() ,
,
所以![]() 的最大正整數值為8.
的最大正整數值為8.
(3)證明:![]() ,
,![]() 且
且![]() ,
,
要證明![]() ,
,
只需證![]() ,
,![]() .
.
即證![]() ,
,
設![]() ,
,
則![]() 時,
時,![]() 恒成立;
恒成立;![]() 時,
時,![]() 恒成立,
恒成立,
當![]() 時,
時,![]() ,
,
![]() ,
,
因為函數![]() 在
在![]() 內單調遞增,且
內單調遞增,且![]() ,∴
,∴![]() ,
,
所以![]() 在
在![]() 時單調遞減,
時單調遞減,
所以![]() ,
,
所以![]() 在
在![]() 內單調遞增,
內單調遞增,
所以![]() ,成立;
,成立;
同理可得![]() 時,
時,![]() 恒成立,
恒成立,
綜上可得,![]() ,
,![]() 且
且![]() ,
,
![]()


科目:高中數學 來源: 題型:
【題目】已知![]() 分別為
分別為![]() 的三內角A,B,C的對邊,其面積
的三內角A,B,C的對邊,其面積![]() ,在等差數列
,在等差數列![]() 中,
中,![]() ,公差
,公差![]() .數列
.數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一商場對每天進店人數和商品銷售件數進行了統計對比,得到如下表格:

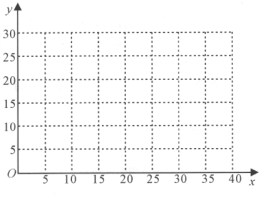
(1)在給定的坐標系中畫出表中數據的散點圖,并由散點圖判斷銷售件數![]() 與進店人數
與進店人數![]() 是否線性相關?(給出判斷即可,不必說明理由)
是否線性相關?(給出判斷即可,不必說明理由)
(2)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測進店人數為80時,商品銷售的件數(結果保留整數).
的回歸方程(系數精確到0.01),預測進店人數為80時,商品銷售的件數(結果保留整數).
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:回歸方程![]() ,其中
,其中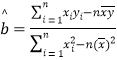 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
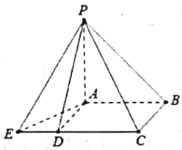
【題目】中國古代數學經典《九章算術》系統地總結了戰國、秦、漢時期的數學成就,書中將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的三棱錐稱之為鱉臑,如圖為一個陽馬與一個鱉臑的組合體,已知![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,
為正方形,![]() ,
,![]() ,若鱉臑
,若鱉臑![]() 的外接球的體積為
的外接球的體積為![]() ,則陽馬
,則陽馬![]() 的外接球的表面積等于______。
的外接球的表面積等于______。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對任意x∈R,存在函數f(x)滿足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com