
【題目】近期,西安公交公司分別推出支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付.某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,![]() 表示活動推出的天數,
表示活動推出的天數,![]() 表示每天使用掃碼支付的人次(單位:十人次),統計數據如表下所示:
表示每天使用掃碼支付的人次(單位:十人次),統計數據如表下所示:
![]()
根據以上數據,繪制了散點圖.
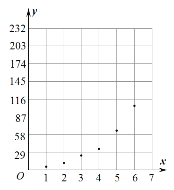
(1)根據散點圖判斷,在推廣期內,![]() 與
與![]() (
(![]() 均為大于零的常數),哪一個適宜作為掃碼支付的人次
均為大于零的常數),哪一個適宜作為掃碼支付的人次![]() 關于活動推出天數
關于活動推出天數![]() 的回歸方程類型?(給出判斷即可,不必說明理由);
的回歸方程類型?(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果及表1中的數據,建立![]() 與
與![]() 的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
(3)推廣期結束后,車隊對乘客的支付方式進行統計,結果如下表:
![]()
西安公交六公司車隊為緩解周邊居民出行壓力,以![]() 萬元的單價購進了一批新車,根據以往的經驗可知,每輛車每個月的運營成本約為
萬元的單價購進了一批新車,根據以往的經驗可知,每輛車每個月的運營成本約為![]() 萬元.已知該線路公交車票價為
萬元.已知該線路公交車票價為![]() 元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受
元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受![]() 折優惠,掃碼支付的乘客隨機優惠,根據統計結果得知,使用掃碼支付的乘客中有
折優惠,掃碼支付的乘客隨機優惠,根據統計結果得知,使用掃碼支付的乘客中有![]() 的概率享受
的概率享受![]() 折優惠,有
折優惠,有![]() 的概率享受
的概率享受![]() 折優惠,有
折優惠,有![]() 的概率享受
的概率享受![]() 折優惠.預計該車隊每輛車每個月有
折優惠.預計該車隊每輛車每個月有![]() 萬人次乘車,根據所給數據以事件發生的頻率作為相應事件發生的概率,在不考慮其它因素的條件下,按照上述收費標準,假設這批車需要
萬人次乘車,根據所給數據以事件發生的頻率作為相應事件發生的概率,在不考慮其它因素的條件下,按照上述收費標準,假設這批車需要![]() (
(![]() )年才能開始盈利,求
)年才能開始盈利,求![]() 的值.
的值.
參考數據:
|
|
|
|
|
|
|
|
|
|
其中其中![]() ,
,![]() ,
,
參考公式:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: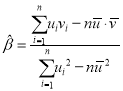 ,
,![]() .
.
【答案】(1)![]() (2)
(2)![]() ,3470(3)7
,3470(3)7
【解析】
(1)由散點圖可知,更接近指數增長,所以![]() 適宜作為掃碼支付的人次
適宜作為掃碼支付的人次![]() 關于活動推出天數
關于活動推出天數![]() 的回歸方程類型.
的回歸方程類型.
(2)根據(1)的判斷結果![]() 兩邊取對數得
兩邊取對數得![]() ,則
,則![]() 兩者線性相關,根據已知條件求出
兩者線性相關,根據已知條件求出![]() 得回歸方程,進而得到y關于x的回歸方程,再令
得回歸方程,進而得到y關于x的回歸方程,再令![]() ,求預測值
,求預測值
(3)設一名乘客一次乘車的費用為![]() 元,根據題意
元,根據題意![]() 得可能取值為:1.4、1.6、1.8、2,求出分布列,進而求得期望,然后再建立不等式求解.
得可能取值為:1.4、1.6、1.8、2,求出分布列,進而求得期望,然后再建立不等式求解.
(1)根據散點圖判斷,在推廣期內, ![]() (
(![]() 均為大于零的常數),適宜作為掃碼支付的人次
均為大于零的常數),適宜作為掃碼支付的人次![]() 關于活動推出天數
關于活動推出天數![]() 的回歸方程類型.
的回歸方程類型.
(2)根據(1)的判斷結果![]() ,
,
兩邊取對數得![]() ,
,
其中![]() ,
,![]() ,
,![]() ,
,
 ,
,
![]() ,
,
所以![]() 。
。
所以![]() 。
。
當![]() 時,
時, ![]() 。
。
所以活動推出第8天使用掃碼支付的人次3470人.
(3)設一名乘客一次乘車的費用為![]() 元,
元,
根據題意![]() 得可能取值為:1.4、1.6、1.8、2
得可能取值為:1.4、1.6、1.8、2
![]() ,
,
![]() ,
,
![]() 。
。
假設這批車需要![]() (
(![]() )年才能開始盈利,
)年才能開始盈利,
則![]() ,
,
解得![]() 。
。
所以需要7年才能開始盈利.。


科目:高中數學 來源: 題型:
【題目】有下列說法:①在殘差圖中,殘差點比較均勻地落在水平的帶狀區域內,說明選用的模型比較合適.②相關指數![]() 來刻畫回歸的效果,
來刻畫回歸的效果,![]() 值越大,說明模型的擬合效果越好.③比較兩個模型的擬合效果,可以比較殘差平方和的大小,殘差平方和越小的模型,擬合效果越好.其中正確命題的個數是( )
值越大,說明模型的擬合效果越好.③比較兩個模型的擬合效果,可以比較殘差平方和的大小,殘差平方和越小的模型,擬合效果越好.其中正確命題的個數是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高三年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率統計表和頻率分布直方圖如下:
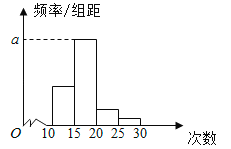
分組 | 頻數 | 頻率 |
| 15 | 0.30 |
| 29 |
|
|
|
|
| 2 |
|
合計 |
| 1 |
(1)求出表中![]() ,
,![]() 及圖中
及圖中![]() 的值;
的值;
(2)若該校高三學生人數有500人,試估計該校高三學生參加社區服務的次數在區間![]() 內的人數;
內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至多一人參加社區服務次數在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與拋物線
與拋物線![]() :
:![]() 的準線交于
的準線交于![]() ,
,![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() :
:![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且曲線
兩點,且曲線![]() 上存在兩點
上存在兩點![]() ,
,![]() 關于直線
關于直線![]() 對稱,求實數
對稱,求實數![]() 的取值范圍及
的取值范圍及![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,![]() ,
,![]() ,
,![]() .
.
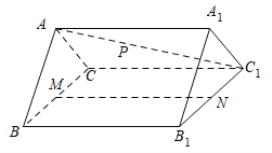
(1)證明:平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,![]() 是線段
是線段![]() 上的動點,若二面角
上的動點,若二面角![]() 的平面角的大小為
的平面角的大小為![]() ,試確定點
,試確定點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,側面
中,側面![]() 是邊長為2的等邊三角形且垂直于底面
是邊長為2的等邊三角形且垂直于底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
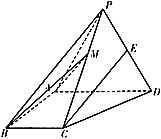
(1)求證:直線![]() 平面
平面![]() ;
;
(2)點![]() 在棱
在棱![]() 上,且二面角
上,且二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與底面
與底面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
在直角坐標系xOy中,設傾斜角為α的直線l:![]() (t為參數)與曲線C:
(t為參數)與曲線C:![]() (θ為參數)相交于不同的兩點A,B.
(θ為參數)相交于不同的兩點A,B.
(Ⅰ)若α=![]() ,求線段AB中點M的坐標;
,求線段AB中點M的坐標;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直線l的斜率.
),求直線l的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com