【題目】如圖所示，已知正方體ABCD－A1B1C1D1.
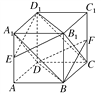
(1)求證：平面A1BD∥平面B1D1C.
(2)若E，F分別是AA1，CC1的中點，求證：平面EB1D1∥平面FBD.
【答案】（1）見解析；（2）見解析
【解析】試題分析：（1）由
，得
，進而證得平面
平面
.
（2）由
，得
，再由
，則
，進而證得
平面
，即可得到結論.
試題解析：
(1)因為
，所以四邊形BB1D1D是平行四邊形，
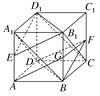
所以B1D1∥BD，又BD平面B1D1C，B1D1平面B1D1C，所以BD∥平面B1D1C.
同理A1D∥平面B1D1C，又A1D∩BD＝D，所以平面A1BD∥平面B1D1C.
(2)由BD∥B1D1，得BD∥平面EB1D1，取BB1的中點G，連接AG，GF，易得AE∥B1G，
又因為AE＝B1G，所以四邊形AEB1G是平行四邊形，所以B1E∥AG.易得GF∥AD.
又因為GF＝AD，所以四邊形ADFG是平行四邊形，所以AG∥DF，所以B1E∥DF，
DF平面EB1D1，B1E平面EB1D1，所以DF∥平面EB1D1.
又因為BD∩DF＝D，所以平面EB1D1∥平面FBD.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】求分別滿足下列條件的直線l的方程：
(1)斜率是
，且與兩坐標軸圍成的三角形的面積是6；
(2)經過兩點A(1,0)、B(m,1)；
(3)經過點(4，－3)，且在兩坐標軸上的截距的絕對值相等．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某省高考改革新方案，不分文理科，高考成績實行“3+3”的構成模式，第一個“3”是語文、數學、外語，每門滿分150分，第二個“3”由考生在思想政治、歷史、地理、物理、化學、生物6個科目中自主選擇其中3個科目參加等級性考試，每門滿分100分，高考錄取成績卷面總分滿分750分．為了調查學生對物理、化學、生物的選考情況，將“某市某一屆學生在物理、化學、生物三個科目中至少選考一科的學生”記作學生群體S，從學生群體S中隨機抽取了50名學生進行調查，他們選考物理，化學，生物的科目數及人數統計如表：
選考物理、化學、生物的科目數 | 1 | 2 | 3 |
人數 | 5 | 25 | 20 |
（I）從所調查的50名學生中任選2名，求他們選考物理、化學、生物科目數量不相等的概率；
（II）從所調查的50名學生中任選2名，記X表示這2名學生選考物理、化學、生物的科目數量之差的絕對值，求隨機變量X的分布列和數學期望；
（III）將頻率視為概率，現從學生群體S中隨機抽取4名學生，記其中恰好選考物理、化學、生物中的兩科目的學生數記作Y，求事件“y≥2”的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】微信紅包是一款可以實現收發紅包、查收記錄和提現的手機應用．某網絡運營商對甲、乙兩個品牌各5種型號的手機在相同環境下，對它們搶到的紅包個數進行統計，得到如表數據：
型號 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌（個） | 4 | 3 | 8 | 6 | 12 |
乙品牌（個） | 5 | 7 | 9 | 4 | 3 |
（Ⅰ）如果搶到紅包個數超過5個的手機型號為“優”，否則“非優”，請據此判斷是否有85%的把握認為搶到的紅包個數與手機品牌有關？
（Ⅱ）如果不考慮其它因素，要從甲品牌的5種型號中選出3種型號的手機進行大規模宣傳銷售．
①求在型號Ⅰ被選中的條件下，型號Ⅱ也被選中的概率；
②以X表示選中的手機型號中搶到的紅包超過5個的型號種數，求隨機變量X的分布列及數學期望E（X）．
下面臨界值表供參考：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式：K2= 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體ABCD－A′B′C′D′的棱長為a，連接A′C′，A′D，A′B，BD，BC′，C′D，得到一個三棱錐.求：
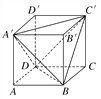
(1)三棱錐A′－BC′D的表面積與正方體表面積的比值；
(2)三棱錐A′－BC′D的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在兩塊鋼板上打孔，用釘帽呈半球形、釘身為圓柱形的鉚釘(圖1)穿在一起，在沒有帽的一端錘打出一個帽，使得與釘帽的大小相等.鉚合的兩塊鋼板，成為某種鋼結構的配件，其截面圖如圖2.(單位：mm，加工中不計損失).
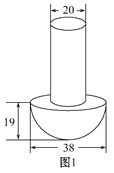
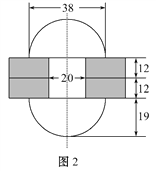
(1)若釘身高度是釘帽高度的2倍，求鉚釘的表面積.
(2)若每塊鋼板的厚度為12mm，求釘身的長度(結果精確到1 mm).
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設命題p：直線mx﹣y+1=0與圓（x﹣2）2+y2=4有公共點；設命題q：實數m滿足方程 
+ 
=1表示雙曲線．
（1）若“p∧q”為真命題，求實數m的取值范圍；
（2）若“p∧q”為假命題，“p∨q”為真命題，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了預防流感，某學校對教室用藥熏消毒法進行消毒.已知藥物釋放過程中，室內每立方米空氣中的含藥量
（毫克）與時間
（小時）成正比；藥物釋放完畢后，
與
的函數關系式為
（
為常數），如圖所示.據圖中提供的信息，回答下列問題：
（1）寫出從藥物釋放開始，每立方米空氣中的含藥量
（毫克）與時間
（小時）之間的函數關系式；
（2）據測定，當空氣中每立方米的含藥量降低到
毫克以下時，學生方可進教室。那么藥物釋放開始，至少需要經過多少小時后，學生才能回到教室？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
