
【題目】已知函數f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e為自然對數的底數)
(a∈R,e為自然對數的底數)
(Ⅰ)當a=1時,求f(x)的單調區間;
(Ⅱ)若函數f(x)在![]() 上無零點,求a的最小值;
上無零點,求a的最小值;
(Ⅲ)若對任意給定的x0∈(0,e],在(0,e]上總存在兩個不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范圍.
【答案】(1) f(x)的單調減區間為(0,2],單調增區間為[2,+∞);(2) 函數f(x)在![]() 上無零點,則a的最小值為2﹣4ln2;(3)a的范圍是
上無零點,則a的最小值為2﹣4ln2;(3)a的范圍是![]() .
.
【解析】試題分析:(Ⅰ)把a=1代入到f(x)中求出f′(x),令f′(x)>0求出x的范圍即為函數的增區間,令f′(x)<0求出x的范圍即為函數的減區間;
(Ⅱ)f(x)<0時不可能恒成立,所以要使函數在(0, ![]() )上無零點,只需要對x∈(0,
)上無零點,只需要對x∈(0, ![]() )時f(x)>0恒成立,列出不等式解出a大于一個函數,利用導數得到函數的單調性,根據函數的增減性得到這個函數的最大值即可得到a的最小值;
)時f(x)>0恒成立,列出不等式解出a大于一個函數,利用導數得到函數的單調性,根據函數的增減性得到這個函數的最大值即可得到a的最小值;
(Ⅲ)求出g′(x),根據導函數的正負得到函數的單調區間,即可求出g(x)的值域,而當a=2時不合題意;當a≠2時,求出f′(x)=0時x的值,根據x∈(0,e]列出關于a的不等式得到①,并根據此時的x的值討論導函數的正負得到函數f(x)的單調區間,根據單調區間得到②和③,令②中不等式的坐標為一個函數,求出此函數的導函數,討論導函數的正負得到函數的單調區間,根據函數的增減性得到此函數的最大值,即可解出②恒成立和解出③得到④,聯立①和④即可解出滿足題意a的取值范圍.
試題解析:
(1)當a=1時,f(x)=x﹣1﹣2lnx,則f′(x)=1﹣![]() ,
,
由f′(x)>0,得x>2;
由f′(x)<0,得0<x<2.
故f(x)的單調減區間為(0,2],單調增區間為[2,+∞);
(2)因為f(x)<0在區間![]() 上恒成立不可能,
上恒成立不可能,
故要使函數![]() 上無零點,
上無零點,
只要對任意的![]() ,f(x)>0恒成立,即對
,f(x)>0恒成立,即對![]() 恒成立.
恒成立.
令![]() ,則
,則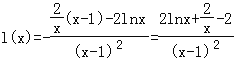 ,
,
再令![]() ,
,
則![]() ,故m(x)在
,故m(x)在![]() 上為減函數,于是
上為減函數,于是![]() ,
,
從而,l(x)>0,于是l(x)在![]() 上為增函數,所以
上為增函數,所以![]() ,
,
故要使![]() 恒成立,只要a∈[2﹣4ln2,+∞),
恒成立,只要a∈[2﹣4ln2,+∞),
綜上,若函數f(x)在![]() 上無零點,則a的最小值為2﹣4ln2;
上無零點,則a的最小值為2﹣4ln2;
(3)g′(x)=e1﹣x﹣xe1﹣x=(1﹣x)e1﹣x,
當x∈(0,1)時,g′(x)>0,函數g(x)單調遞增;
當x∈(1,e]時,g′(x)<0,函數g(x)單調遞減.
又因為g(0)=0,g(1)=1,g(e)=ee1﹣e>0,
所以,函數g(x)在(0,e]上的值域為(0,1].
當a=2時,不合題意;
當a≠2時,f′(x)= ,x∈(0,e]
,x∈(0,e]
當x=![]() 時,f′(x)=0.
時,f′(x)=0.
由題意得,f(x)在(0,e]上不單調,故![]() ,即
,即![]() ①
①
此時,當x變化時,f′(x),f(x)的變化情況如下:
x | (0, |
| ( |
f′(x) | ﹣ | 0 | + |
f(x) | ↘ | 最小值 | ↗ |
又因為,當x→0時,2﹣a>0,f(x)→+∞,
![]() ,
,
所以,對任意給定的x0∈(0,e],在(0,e]上總存在兩個不同的xi(i=1,2),
使得f(xi)=g(x0)成立,當且僅當a滿足下列條件:
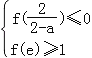 即
即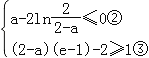
令h(a)=![]() ,
,
則h![]() ,令h′(a)=0,得a=0或a=2,
,令h′(a)=0,得a=0或a=2,
故當a∈(﹣∞,0)時,h′(a)>0,函數h(a)單調遞增;
當![]() 時,h′(a)<0,函數h(a)單調遞減.
時,h′(a)<0,函數h(a)單調遞減.
所以,對任意![]() ,有h(a)≤h(0)=0,
,有h(a)≤h(0)=0,
即②對任意![]() 恒成立.
恒成立.
由③式解得:![]() .④
.④
綜合①④可知,當a的范圍是![]() 時,對任意給定的x0∈(0,e],在(0,e]上總存在兩個不同的xi(i=1,2),使f(xi)=g(x0)成立.
時,對任意給定的x0∈(0,e],在(0,e]上總存在兩個不同的xi(i=1,2),使f(xi)=g(x0)成立.


科目:高中數學 來源: 題型:
【題目】根據下列條件,分別求直線方程:
(1)經過點A(3,0)且與直線2x+y﹣5=0垂直;
(2)求經過直線x﹣y﹣1=0與2x+y﹣2=0的交點,且平行于直線x+2y﹣3=0的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公比不為1的等比數列{an}的前5項積為243,且2a3為3a2和a4的等差中項.
(1)求數列{an}的通項公式an;
(2)若數列{bn}滿足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求數列 ![]() 的前n項和Sn .
的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+lnx(a∈R).
(1)當a=![]() 時,求f(x)在區間[1,e]上的最大值和最小值;
時,求f(x)在區間[1,e]上的最大值和最小值;
(2)如果函數g(x),f1(x),f2(x),在公共定義域D上,滿足f1(x)<g(x)<f2(x),那么就稱g(x)為f1(x),f2(x)的“活動函數”.已知函數![]() .
. ![]() 。若在區間(1,+∞)上,函數f(x)是f1(x),f2(x)的“活動函數”,求a的取值范圍.
。若在區間(1,+∞)上,函數f(x)是f1(x),f2(x)的“活動函數”,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內角A,B,C的對邊,c= ![]() asinC﹣ccosA.
asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面積為 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高三年級有學生500人,其中男生300人,女生200人,為了研究學生的數學成績是否與性別有關,現采用分層抽樣的方法,從中抽取了100名學生,先統計了他們期中考試的數學分數,然后按性別分為男、女兩組,再將兩組學生的分數分成5組:[100,110),[110,120),[120,130),[130,140),[140,150]分別加以統計,得到如圖所示的頻率分布直方圖. 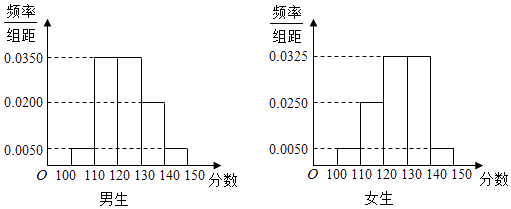
附:K2= ![]() .
.
(1)從樣本中分數小于110分的學生中隨機抽取2人,求兩人恰好為一男一女的概率;
(2)若規定分數不小于130分的學生為“數學尖子生”,請你根據已知條件完成2×2列聯表,并判斷是否有90%的把握認為“數學尖子生與性別有關”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
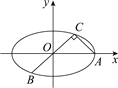
【題目】已知A,B,C是橢圓C: ![]() (a>b>0)上的三點,其中點A的坐標為(2
(a>b>0)上的三點,其中點A的坐標為(2![]() ,0),BC過橢圓的中心,且
,0),BC過橢圓的中心,且![]() ·
·![]() =0,|
=0,|![]() |=2|
|=2|![]() |
|
(1)求橢圓C的方程;
(2)過點(0,t)的直線l(斜率存在)與橢圓C交于P,Q兩點,設D為橢圓C與y軸負半軸的交點,且|![]() |=|
|=|![]() |,求實數t的取值范圍.
|,求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com