
【題目】【2017福建三明5月質檢】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
科目:高中數學 來源: 題型:
【題目】已知集合A,B滿足,集合A={x|x=7k+3,k∈N},B={x|x=7k﹣4,k∈Z},則A,B兩個集合的關系:AB(橫線上填入,或=)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知U={1,2,3,4,5,6,7,8},A={1,3,5,7},B={2,4,5}則U(A∪B)( )
A.{6,8}
B.{5,7}
C.{4,6,7}
D.{1,3,5,6,8}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017江西4月質檢】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
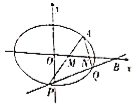
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 且斜率大于0的直線
且斜率大于0的直線![]() 與橢圓
與橢圓![]() 相交于點
相交于點![]() ,
,![]() ,直線
,直線![]() ,
,![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊矩形空地,要在這塊空地上辟一個內接四邊形為綠地,使其四個頂點分別落在矩形的四條邊上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,設AE=x,綠地面積為y. 
(1)寫出y關于x的函數關系式,并指出這個函數的定義域.
(2)當AE為何值時,綠地面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017廣東佛山二模】某保險公司針對企業職工推出一款意外險產品,每年每人只要交少量保費,發生意外后可一次性獲賠50萬元.保險公司把職工從事的所有崗位共分為![]() 、
、![]() 、
、![]() 三類工種,根據歷史數據統計出三類工種的每賠付頻率如下表(并以此估計賠付概率).
三類工種,根據歷史數據統計出三類工種的每賠付頻率如下表(并以此估計賠付概率).


(Ⅰ)根據規定,該產品各工種保單的期望利潤都不得超過保費的20%,試分別確定各類工種每張保單保費的上限;
(Ⅱ)某企業共有職工20000人,從事三類工種的人數分布比例如圖,老板準備為全體職工每人購買一份此種保險,并以(Ⅰ)中計算的各類保險上限購買,試估計保險公司在這宗交易中的期望利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過長期觀測得到:在交通繁忙的時段內,某公路段汽車的車流量y(千輛/小時)與汽車的平均速度υ(千米/小時)之間的函數關系為:y= ![]() (υ>0).
(υ>0).
(1)在該時段內,當汽車的平均速度υ為多少時,車流量最大?最大車流量為多少?(保留分數形式)
(2)若要求在該時段內車流量超過10千輛/小時,則汽車的平均速度應在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017四川資陽4月模擬】共享單車是指由企業在校園、公交站點、商業區、公共服務區等場所提供的自行車單車共享服務,由于其依托“互聯網+”,符合“低碳出行”的理念,已越來越多地引起了人們的關注.某部門為了對該城市共享單車加強監管,隨機選取了100人就該城市共享單車的推行情況進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照[50,60),[60,70),…,[90,100]分成5組,制成如圖所示頻率分直方圖.
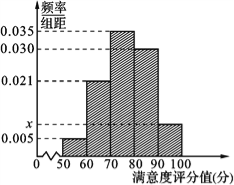
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)已知滿意度評分值在[90,100]內的男生數與女生數的比為2:1,若在滿意度評分值為[90,100]的人中隨機抽取4人進行座談,設其中的女生人數為隨機變量X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列
(1)在等差數列{an}中,a6=10,S5=5,求該數列的第8項a8;
(2)在等比數列{bn}中,b1+b3=10,b4+b6= ![]() ,求該數列的前5項和S5 .
,求該數列的前5項和S5 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com