
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若![]() 恒成立,試確定實數
恒成立,試確定實數![]() 的取值范圍;
的取值范圍;
(3)證明: ![]()
![]() .
.
 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】定義非零向量![]() 的“相伴函數”為
的“相伴函數”為![]() (
(![]() ),向量
),向量![]() 稱為函數
稱為函數![]() 的“相伴向量”(其中
的“相伴向量”(其中![]() 為坐標原點),記平面內所有向量的“相伴函數”構成的集合為
為坐標原點),記平面內所有向量的“相伴函數”構成的集合為![]() .
.
(1)已知![]() (
(![]() ),求證:
),求證:![]() ,并求函數
,并求函數![]() 的“相伴向量”模的取值范圍;
的“相伴向量”模的取值范圍;
(2)已知點![]() (
(![]() )滿足
)滿足![]() ,向量
,向量![]() 的 “相伴函數”
的 “相伴函數”![]() 在
在![]() 處取得最大值,當點
處取得最大值,當點![]() 運動時,求
運動時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位將舉辦慶典活動,要在廣場上豎立一形狀為等腰梯形的彩門BADC (如圖),設計要求彩門的面積為S (單位:m2)高為h(單位:m)(S,h為常數),彩門的下底BC固定在廣場地面上,上底和兩腰由不銹鋼支架構成,設腰和下底的夾角為α,不銹鋼支架的長度和記為l. 
(1)請將l表示成關于α的函數l=f(α);
(2)問當α為何值時l最小?并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數f(x)=(x+l)lnx﹣ax+a (a為正實數,且為常數)
(1)若f(x)在(0,+∞)上單調遞增,求a的取值范圍;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分10分)已知等差數列{an}滿足a1+a2=10,a4-a3=2.
(1)求{an}的通項公式.
(2)設等比數列{bn}滿足b2=a3,b3=a7.問:b6與數列{an}的第幾項相等?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京市某年11月1日—20日監測最高最低溫度及差值數據如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高溫度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低溫度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的頻率分布表及頻率分布直方圖,并寫出頻率分布直方圖中![]() 的值;
的值;

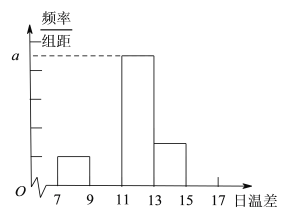
(Ⅱ)從日溫差大于等于![]() 的這些天中,隨機選取2天.求這兩天中至少有一天的溫差在區間
的這些天中,隨機選取2天.求這兩天中至少有一天的溫差在區間![]() 內的概率.
內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com