
���}Ŀ���O(sh��)![]() �M��s���l��
�M��s���l��![]() ��
��![]() ����Сֵ��7���t
����Сֵ��7���t![]() ��_________.
��_________.
���𰸡�3
��������
����(j��)�s���l����(hu��)���������ٰ�Ŀ��(bi��o)����(sh��)�D(zhu��n)����![]() ����(du��)����(sh��)a���ӑՓ����(d��ng)
����(du��)����(sh��)a���ӑՓ����(d��ng)![]() �r(sh��)�@Ȼ���M���}�⣻��(d��ng)
�r(sh��)�@Ȼ���M���}�⣻��(d��ng)![]() �r(sh��)��ֱ��
�r(sh��)��ֱ��![]() ��(j��ng)�^(gu��)�������е��c(di��n)A�r(sh��)���ؾ���С����z����Сֵ��������Сֵ��7���ó��Y(ji��)������(d��ng)
��(j��ng)�^(gu��)�������е��c(di��n)A�r(sh��)���ؾ���С����z����Сֵ��������Сֵ��7���ó��Y(ji��)������(d��ng)![]() �r(sh��)��
�r(sh��)��![]() �Ľؾ��](m��i)����Сֵ����z�](m��i)����Сֵ����(d��ng)
�Ľؾ��](m��i)����Сֵ����z�](m��i)����Сֵ����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() �Ľؾ��](m��i)�����ֵ����z�](m��i)����Сֵ���C�Ͽɵó��Y(ji��)��.
�Ľؾ��](m��i)�����ֵ����z�](m��i)����Сֵ���C�Ͽɵó��Y(ji��)��.
����(j��)�s���l����(hu��)�����������£���![]() ���ɵó����c(di��n)
���ɵó����c(di��n)![]() ��
��
��![]() �ɵ�
�ɵ�![]() ����(d��ng)
����(d��ng)![]() �r(sh��)�@Ȼ���M���}�⣻
�r(sh��)�@Ȼ���M���}�⣻
��(d��ng)![]() ��
��![]() �r(sh��)���ɿ������֪��(d��ng)ֱ��
�r(sh��)���ɿ������֪��(d��ng)ֱ��![]() ��(j��ng)�^(gu��)�������е��c(di��n)A�r(sh��)���ؾ���С����z����Сֵ����
��(j��ng)�^(gu��)�������е��c(di��n)A�r(sh��)���ؾ���С����z����Сֵ����![]() �����
�����![]() ��
��![]() ���ᣩ��
���ᣩ��
��(d��ng)![]() ��
��![]() �r(sh��)���ɿ������֪
�r(sh��)���ɿ������֪![]() �Ľؾ��](m��i)����Сֵ����z�](m��i)����Сֵ��
�Ľؾ��](m��i)����Сֵ����z�](m��i)����Сֵ��
��(d��ng)![]() ��
��![]() �r(sh��)������(j��)�������֪
�r(sh��)������(j��)�������֪![]() �Ľؾ��](m��i)�����ֵ����z�](m��i)����Сֵ.
�Ľؾ��](m��i)�����ֵ����z�](m��i)����Сֵ.
�C�Ͽ�֪�M��l���r(sh��)![]() .
.
�ʴ𰸞飺3.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����![]() �У�����(g��)��(n��i)�ǵČ�(du��)߅�քe��a��b��c��
�У�����(g��)��(n��i)�ǵČ�(du��)߅�քe��a��b��c��![]() ��
��![]() ��
��
![]() ��B��ֵ��
��B��ֵ��
![]() �O(sh��)
�O(sh��)![]() ����
����![]() ����eS��
����eS��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�p����![]() ��һ��(g��)���c(di��n)��
��һ��(g��)���c(di��n)��![]() ����
����![]()
��1�����p����![]() �ķ���
�ķ���
��2���O(sh��)��(j��ng)�^(gu��)���c(di��n)![]() ��ֱ��
��ֱ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() ����(d��ng)ֱ��
����(d��ng)ֱ��![]() �c�p����
�c�p����![]() ����֧�ཻ�ڲ�ͬ�ă��c(di��n)
����֧�ཻ�ڲ�ͬ�ă��c(di��n)![]() �r(sh��)����(sh��)��(sh��)
�r(sh��)����(sh��)��(sh��)![]() ��ȡֵ����
��ȡֵ����
��3���O(sh��)��2����ֱ��![]() �c�p����
�c�p����![]() ����֧�ཻ��
����֧�ཻ��![]() ���c(di��n)����(w��n)�Ƿ���ڌ�(sh��)��(sh��)
���c(di��n)����(w��n)�Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ��
��ʹ��![]() ���J�ǣ������ڣ�Ո(q��ng)���
���J�ǣ������ڣ�Ո(q��ng)���![]() �ķ������������ڣ�Ո(q��ng)�f(shu��)������
�ķ������������ڣ�Ո(q��ng)�f(shu��)������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����![]() �Ķ��(xi��ng)չ�_(k��i)ʽ�У������(xi��ng)�Ķ��(xi��ng)ʽϵ��(sh��)֮�͞�
�Ķ��(xi��ng)չ�_(k��i)ʽ�У������(xi��ng)�Ķ��(xi��ng)ʽϵ��(sh��)֮�͞�![]() .
.
��1����չ�_(k��i)ʽ�ij���(sh��)�(xi��ng)��
��2����չ�_(k��i)ʽ�������攵(sh��)�(xi��ng)��ϵ��(sh��)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�������_�Ă�(g��)��(sh��)�ǣ� ��
�����P(gu��n)ϵ��(sh��)![]() �Á�(l��i)����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)����
�Á�(l��i)����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)����![]() Խ�ӽ���1�����P(gu��n)��Խ����
Խ�ӽ���1�����P(gu��n)��Խ����
�ڻؚwֱ��![]() �^(gu��)�ӱ��c(di��n)����
�^(gu��)�ӱ��c(di��n)����![]() ��
��
�����P(gu��n)ָ��(sh��)![]() �Á�(l��i)�̮�(hu��)�ؚw��Ч����
�Á�(l��i)�̮�(hu��)�ؚw��Ч����![]() ԽС���f(shu��)��ģ�͵ĔM��Ч��Խ����.
ԽС���f(shu��)��ģ�͵ĔM��Ч��Խ����.
A. 0B. 1C. 2D. 3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�����_����______�����������_����̖(h��o)����(xi��)����
��1��ֱ��![]() ��ƽ��
��ƽ��![]() ����
����![]() ��
��![]() ���t
���t![]() ��
��
��2����ͬƽ��![]() ��������
��������![]() ���t
���t![]() ������
������![]() ��ֱ������
��ֱ������![]() ��
��
��3����֪![]() ���t
���t![]() ��
��
��4��ƽ��![]() ��ƽ��
��ƽ��![]() ���t
���t![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
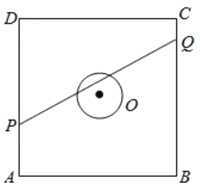
���}Ŀ����D��������![]() ��߅�L(zh��ng)��
��߅�L(zh��ng)��![]() �ף��A
�ף��A![]() �İ돽��
�İ돽��![]() �ף��A���������ε����ģ��c(di��n)
�ף��A���������ε����ģ��c(di��n)![]() ��
��![]() �քe�ھ���
�քe�ھ���![]() ��
��![]() �ϣ�������
�ϣ�������![]() �c�A
�c�A![]() ����c(di��n)���t�Q�c(di��n)
����c(di��n)���t�Q�c(di��n)![]() ���c(di��n)
���c(di��n)![]() �ġ�ä�^(q��)���У���֪�c(di��n)
�ġ�ä�^(q��)���У���֪�c(di��n)![]() ��
��![]() ��/����ٶȏ�
��/����ٶȏ�![]() ���l(f��)��
���l(f��)��![]() �Ƅ�(d��ng)��ͬ�r(sh��)���c(di��n)
�Ƅ�(d��ng)��ͬ�r(sh��)���c(di��n)![]() ��
��![]() ��/����ٶȏ�
��/����ٶȏ�![]() ���l(f��)��
���l(f��)��![]() �Ƅ�(d��ng)���t���c(di��n)
�Ƅ�(d��ng)���t���c(di��n)![]() ��
��![]() �Ƅ�(d��ng)��
�Ƅ�(d��ng)��![]() ���^(gu��)���У��c(di��n)
���^(gu��)�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ��ä�^(q��)�еĕr(sh��)�L(zh��ng)�s________�루���_��
��ä�^(q��)�еĕr(sh��)�L(zh��ng)�s________�루���_��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ��
��![]() ���x���ʞ�
���x���ʞ�![]() �������c(di��n)F1�����(zh��n)���ľ��x��4��
�������c(di��n)F1�����(zh��n)���ľ��x��4��

��1����E�A![]() �ķ��̣�
�ķ��̣�
��2�����cԭ�c(di��n)���x��1��ֱ��l1��![]() �c�E�A
�c�E�A![]() �ཻ��A��B���c(di��n)��ֱ��l2�cl1ƽ�У����c�E�A
�ཻ��A��B���c(di��n)��ֱ��l2�cl1ƽ�У����c�E�A![]() �������c(di��n)M��O��Mλ��ֱ��l1�ăɂ�(c��)����ӛ��MAB����OAB����e�քe��S1��S2����
�������c(di��n)M��O��Mλ��ֱ��l1�ăɂ�(c��)����ӛ��MAB����OAB����e�քe��S1��S2����![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�У�������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ������
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ������![]() ��
��![]() .
.
��1�����^(gu��)ԭ�c(di��n)��ֱ���ăAб��![]() �酢��(sh��)����(xi��)������
�酢��(sh��)����(xi��)������![]() �ą���(sh��)���̣�
�ą���(sh��)���̣�
��2��ֱ��![]() �^(gu��)ԭ�c(di��n)�����c����
�^(gu��)ԭ�c(di��n)�����c����![]() ��
��![]() �քe����
�քe����![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ��
��![]() ����ԭ�c(di��n)������
����ԭ�c(di��n)������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com