解:(1)∵關(guān)于x的不等式f(x)<(2m-1)x+1-m
2的解集為(m,m+1),
即不等式x
2+(a+1-2m)x+m
2+m<0的解集為(m,m+1),
∴x
2+(a+1-2m)x+m
2+m=(x-m)(x-m-1).
∴x
2+(a+1-2m)x+m
2+m=x
2-(2m+1)x+m(m+1).
∴a+1-2m=-(2m+1).
∴a=-2.…(2分)
(2)解法1:由(1)得
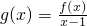
=
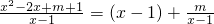
.
∴φ(x)=g(x)-kln(x-1)=
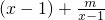
-kln(x-1)的定義域為(1,+∞).
∴φ'(x)=1-
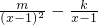
=
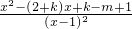
.…(3分)
方程x
2-(2+k)x+k-m+1=0(*)的判別式△=(2+k)
2-4(k-m+1)=k
2+4m.…(4分)
①當m>0時,△>0,方程(*)的兩個實根為
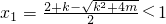
,
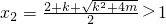
,…(5分)
則x∈(1,x
2)時,φ'(x)<0;x∈(x
2,+∞)時,φ'(x)>0.
∴函數(shù)φ(x)在(1,x
2)上單調(diào)遞減,在(x
2,+∞)上單調(diào)遞增.
∴函數(shù)φ(x)有極小值點x
2.…(6分)
②當m<0時,由△>0,得
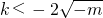
或
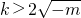
,
若
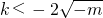
,則
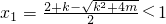
,
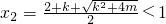
,
故x∈(1,+∞)時,φ'(x)>0,(蘇元高考吧:www.gaokao8.net)
∴函數(shù)φ(x)在(1,+∞)上單調(diào)遞增.
∴函數(shù)φ(x)沒有極值點.…(7分)
若
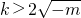
時,
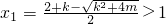
,
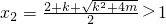
,
則x∈(1,x
1)時,φ'(x)>0;x∈(x
1,x
2)時,φ'(x)<0;x∈(x
2,+∞)時,φ'(x)>0.
∴函數(shù)φ(x)在(1,x
1)上單調(diào)遞增,在(x
1,x
2)上單調(diào)遞減,在(x
2,+∞)上單調(diào)遞增.
∴函數(shù)φ(x)有極小值點x
2,有極大值點x
1.…(8分)
綜上所述,當m>0時,k取任意實數(shù),函數(shù)φ(x)有極小值點x
2;
當m<0時,
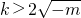
,函數(shù)φ(x)有極小值點x
2,有極大值點x
1.…(9分)
(其中
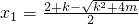
,
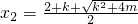
)
解法2:由(1)得
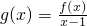
=
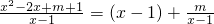
.
∴φ(x)=g(x)-kln(x-1)=
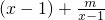
-kln(x-1)的定義域為(1,+∞).
∴φ'(x)=1-
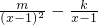
=
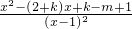
.…(3分)
若函數(shù)φ(x)=g(x)-kln(x-1)存在極值點等價于函數(shù)φ'(x)有兩個不等的零點,且
至少有一個零點在(1,+∞)上.…(4分)
令φ'(x)=
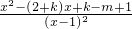
=0,
得x
2-(2+k)x+k-m+1=0,(*)
則△=(2+k)
2-4(k-m+1)=k
2+4m>0,(**) …(5分)
方程(*)的兩個實根為
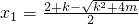
,
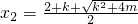
.
設h(x)=x
2-(2+k)x+k-m+1,
①若x
1<1,x
2>1,則h(1)=-m<0,得m>0,此時,k取任意實數(shù),(**)成立.
則x∈(1,x
2)時,φ'(x)<0;x∈(x
2,+∞)時,φ'(x)>0.
∴函數(shù)φ(x)在(1,x
2)上單調(diào)遞減,在(x
2,+∞)上單調(diào)遞增.
∴函數(shù)φ(x)有極小值點x
2.…(6分)
②若x
1>1,x
2>1,則

得
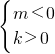
又由(**)解得
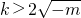
或
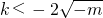
,
故
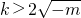
.…(7分)
則x∈(1,x
1)時,φ'(x)>0;x∈(x
1,x
2)時,φ'(x)<0;x∈(x
2,+∞)時,φ'(x)>0.
∴函數(shù)φ(x)在(1,x
1)上單調(diào)遞增,在(x
1,x
2)上單調(diào)遞減,在(x
2,+∞)上單調(diào)遞增.
∴函數(shù)φ(x)有極小值點x
2,有極大值點x
1.…(8分)
綜上所述,當m>0時,k取任何實數(shù),函數(shù)φ(x)有極小值點x
2;
當m<0時,
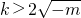
,函數(shù)φ(x)有極小值點x
2,有極大值點x
1.…(9分)
(其中
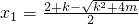
,
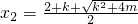
)
(3)證法1:∵m=1,∴g(x)=

.
∴

=
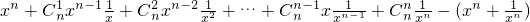
=
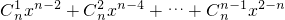
.…(10分)
令T=
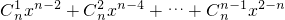
,
則T=

=
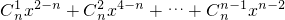
.
∵x>0,
∴2T=
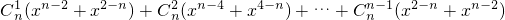
…(11分)≥

…(12分)
=

=
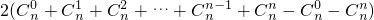
=2(2
n-2).…(13分)
∴T≥2
n-2,即[g(x+1)]
n-g(x
n+1)≥2
n-2.…(14分)
證法2:下面用數(shù)學歸納法證明不等式
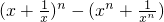
≥2
n-2.
①當n=1時,左邊=

,右邊=2
1-2=0,不等式成立;
…(10分)
②假設當n=k(k∈N
*)時,不等式成立,即
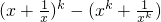
≥2
k-2,
則
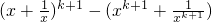
=

=

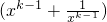
…(11分)
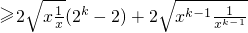
=2
k+1-2.…(13分)
也就是說,當n=k+1時,不等式也成立.
由①②可得,對?n∈N
*,[g(x+1)]
n-g(x
n+1)≥2
n-2都成立.…(14分)
分析:(1)根據(jù)關(guān)于x的不等式f(x)<(2m-1)x+1-m
2的解集為(m,m+1),即不等式x
2+(a+1-2m)x+m
2+m<0的解集為(m,m+1),從而有x
2+(a+1-2m)x+m
2+m=(x-m)(x-m-1).化簡后對照系數(shù)即可得出a的值;
(2)由(1)得
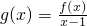
=
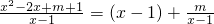
.利用導數(shù)研究其單調(diào)性,從而得出極值的情形;
(3)當m=1時g(x)=

.利用二項定理化簡式子[g(x+1)]
n-g(x
n+1),再利用組合數(shù)的性質(zhì)或數(shù)學歸納法進行證明即得對?n∈N
*,[g(x+1)]
n-g(x
n+1)≥2
n-2都成立.
點評:本小題主要考查二次函數(shù)、一元二次不等式、一元二次方程、函數(shù)應用、均值不等式等基礎知識,考查數(shù)形結(jié)合、函數(shù)與方程、分類與整合、化歸與轉(zhuǎn)化的數(shù)學思想方法,以及抽象概括能力、推理論證能力、運算求解能力、創(chuàng)新意識.

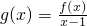 .
.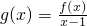 =
=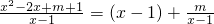 .
.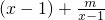 -kln(x-1)的定義域為(1,+∞).
-kln(x-1)的定義域為(1,+∞).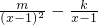 =
=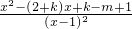 .…(3分)
.…(3分)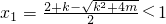 ,
,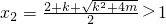 ,…(5分)
,…(5分)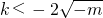 或
或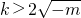 ,
,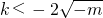 ,則
,則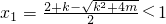 ,
,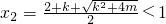 ,
,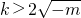 時,
時,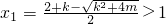 ,
,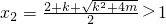 ,
,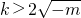 ,函數(shù)φ(x)有極小值點x2,有極大值點x1.…(9分)
,函數(shù)φ(x)有極小值點x2,有極大值點x1.…(9分)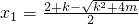 ,
,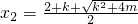 )
)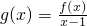 =
=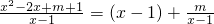 .
.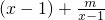 -kln(x-1)的定義域為(1,+∞).
-kln(x-1)的定義域為(1,+∞).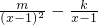 =
=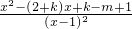 .…(3分)
.…(3分)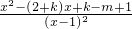 =0,
=0,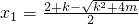 ,
,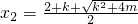 .
. 得
得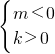
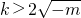 或
或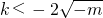 ,
,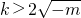 .…(7分)
.…(7分)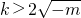 ,函數(shù)φ(x)有極小值點x2,有極大值點x1.…(9分)
,函數(shù)φ(x)有極小值點x2,有極大值點x1.…(9分)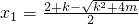 ,
,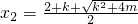 )
) .
. =
=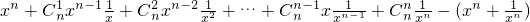
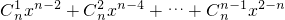 .…(10分)
.…(10分)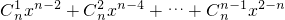 ,
, =
=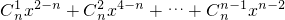 .
.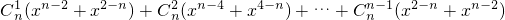 …(11分)≥
…(11分)≥ …(12分)
…(12分) =
=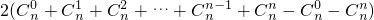 =2(2n-2).…(13分)
=2(2n-2).…(13分)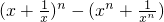 ≥2n-2.
≥2n-2. ,右邊=21-2=0,不等式成立;
,右邊=21-2=0,不等式成立;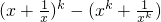 ≥2k-2,
≥2k-2,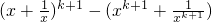 =
= =
=
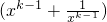 …(11分)
…(11分)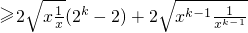 =2k+1-2.…(13分)
=2k+1-2.…(13分)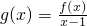 =
=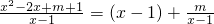 .利用導數(shù)研究其單調(diào)性,從而得出極值的情形;
.利用導數(shù)研究其單調(diào)性,從而得出極值的情形; .利用二項定理化簡式子[g(x+1)]n-g(xn+1),再利用組合數(shù)的性質(zhì)或數(shù)學歸納法進行證明即得對?n∈N*,[g(x+1)]n-g(xn+1)≥2n-2都成立.
.利用二項定理化簡式子[g(x+1)]n-g(xn+1),再利用組合數(shù)的性質(zhì)或數(shù)學歸納法進行證明即得對?n∈N*,[g(x+1)]n-g(xn+1)≥2n-2都成立.

 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案