
【題目】已知函數![]() 。
。
(1)若函數![]() 的一個極值點為
的一個極值點為![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若![]() ,且關于
,且關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍。
的取值范圍。
【答案】(1) ![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() 的單調遞減區間為
的單調遞減區間為![]() 。(2)
。(2) ![]()
【解析】
(1)根據函數的極值點,求得![]() 的值,得到函數
的值,得到函數![]() 解析式,利用導數的符號,即可求得函數的單調區間;
解析式,利用導數的符號,即可求得函數的單調區間;
(2)當![]() 時,
時,![]() 符合題意,
符合題意,
當![]() 時,
時, ![]() ,該方程有一正一負根,即存在
,該方程有一正一負根,即存在![]() ,使得
,使得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,結合
上單調遞增,結合![]() ,求得
,求得![]() 的取值范圍,即可求得
的取值范圍,即可求得![]() 的范圍.
的范圍.
(1)依題可知函數![]() 的定義域為
的定義域為![]() ,且
,且![]() ,
,
因為 函數![]() 的一個極值點為
的一個極值點為![]() ,所以
,所以![]() ,即
,即![]() ,得
,得![]() ,
,
經檢驗,符合題意,所以![]() ,
,
所以 ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() 即
即![]() ,解得
,解得![]() ,
,
所以![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
(2)當![]() 時,
時,![]() 符合題意,
符合題意,
當![]() 時,
時,![]() ,令
,令![]() ,
,
因為![]() ,所以
,所以![]() ,則該方程有兩不同實根,且一正一負,
,則該方程有兩不同實根,且一正一負,
即存在![]() ,使得
,使得![]() ,
,
可知![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]()
![]() ,
,
所以![]() ,即
,即![]() ,
,
因為![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]() 時,
時,![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,
,
設![]() ,則
,則 ,故
,故![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,即為
,即為![]() 的范圍,
的范圍,
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,已知矩形![]() 中,
中,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,若
,若![]() 是線段
是線段![]() 的中點,則
的中點,則![]() 在翻折過程中,下列命題:
在翻折過程中,下列命題:

①線段![]() 的長是定值;
的長是定值;
②存在某個位置,使![]() ;
;
③點![]() 的運動軌跡是一個圓;
的運動軌跡是一個圓;
④存在某個位置,使得![]() 面
面![]() .
.
正確的個數是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年中央電視臺春節聯歡晚會分會場之一落戶黔東南州黎平縣肇興侗寨,黔東南州某中學高二社會實踐小組就社區群眾春晚節目的關注度進行了調查,隨機抽取80名群眾進行調查,將他們的年齡分成6段: ![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
, ![]() ,得到如圖所示的頻率分布直方圖.問:
,得到如圖所示的頻率分布直方圖.問:

(Ⅰ)求這80名群眾年齡的中位數;
(Ⅱ)若用分層抽樣的方法從年齡在![]() 中的群眾隨機抽取6名,并從這6名群眾中選派3人外出宣傳黔東南,求選派的3名群眾年齡在
中的群眾隨機抽取6名,并從這6名群眾中選派3人外出宣傳黔東南,求選派的3名群眾年齡在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
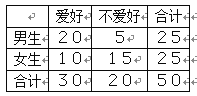
【題目】通過隨機詢問50名性別不同的大學生是否愛好某項運動,得到如下的列聯表,由![]() 得
得![]()
參照附表,得到的正確結論是

A. 有99.5%以上的把握認為“愛好該項運動與性別有關”
B. 有99.5%以上的把握認為“愛好該項運動與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校課題組為了研究學生的數學成績與學生細心程度的關系,在本校隨機調查了100名學生進行研究.研究結果表明:在數學成績及格的60名學生中有45人比較細心,另外15人比較粗心;在數學成績不及格的40名學生中有10人比較細心,另外30人比較粗心.
(I)試根據上述數據完成![]() 列聯表:
列聯表:

(II)能否在犯錯誤的概率不超過0.001的前提下認為學生的數學成績與細心程度有關系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區間
在區間![]() 上為單調遞增函數,求
上為單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的導函數.若正常數
的導函數.若正常數![]() 滿足條件
滿足條件![]() .證明:
.證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com