
已知 、
、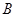 兩盒中都有紅球、白球,且球的形狀、大小都相同,盒子
兩盒中都有紅球、白球,且球的形狀、大小都相同,盒子 中有
中有 個紅球與
個紅球與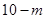 個白球,盒子
個白球,盒子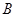 中有
中有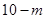 個紅球與
個紅球與 個白球(
個白球(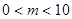 ).
).
(1)分別從 、
、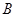 中各取一個球,
中各取一個球, 表示紅球的個數;
表示紅球的個數;
①請寫出隨機變量 的分布列,并證明
的分布列,并證明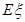 等于定值;
等于定值;
②當 為何值時,
為何值時,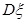 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3個球,事件
中不放回地摸取3個球,事件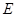 :在第一次取到紅球后,以后兩次都取到白球,事件
:在第一次取到紅球后,以后兩次都取到白球,事件 :在第一次取到白球后,以后兩次都取到紅球,若概率
:在第一次取到白球后,以后兩次都取到紅球,若概率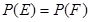 ,求
,求 的值.
的值.
科目:高中數學 來源: 題型:解答題
在乒乓球比賽中,甲與乙以“五局三勝”制進行比賽,根據以往比賽情況,甲在每一局勝乙的概率均為  .已知比賽中,乙先贏了第一局,求:
.已知比賽中,乙先贏了第一局,求:
(Ⅰ)甲在這種情況下取勝的概率;
(Ⅱ)設比賽局數為X,求X的分布列及數學期望(均用分數作答)。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
去年2月29日,我國發布了新修訂的《環境空氣質量標準》指出空氣質量指數在 為優秀,各類人群可正常活動.惠州市環保局對我市2014年進行為期一年的空氣質量監測,得到每天的空氣質量指數,從中隨機抽取50個作為樣本進行分析報告,樣本數據分組區間為
為優秀,各類人群可正常活動.惠州市環保局對我市2014年進行為期一年的空氣質量監測,得到每天的空氣質量指數,從中隨機抽取50個作為樣本進行分析報告,樣本數據分組區間為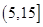 ,
,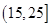 ,
,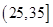 ,
,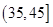 ,由此得到樣本的空氣質量指數頻率分布直方圖,如圖.
,由此得到樣本的空氣質量指數頻率分布直方圖,如圖.
(1) 求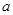 的值;
的值;
(2) 根據樣本數據,試估計這一年度的空氣質量指數的平均值;(注:設樣本數據第 組的頻率為
組的頻率為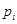 ,第
,第 組區間的中點值為
組區間的中點值為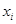
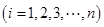 ,則樣本數據的平均值為
,則樣本數據的平均值為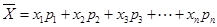 .)
.)
(3) 如果空氣質量指數不超過 ,就認定空氣質量為“特優等級”,則從這一年的監測數據中隨機抽取
,就認定空氣質量為“特優等級”,則從這一年的監測數據中隨機抽取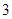 天的數值,其中達到“特優等級”的天數為
天的數值,其中達到“特優等級”的天數為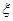 ,求
,求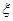 的分布列和數學期望.
的分布列和數學期望.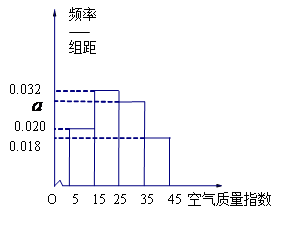
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
小王經營一家面包店,每天從生產商處訂購一種品牌現烤面包出售.已知每賣出一個現烤面包可獲利10元,若當天賣不完,則未賣出的現烤面包因過期每個虧損5元.經統計,得到在某月(30天)中,小王每天售出的現烤面包個數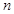 及天數如下表:
及天數如下表:
售出個數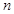 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天數 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
我國政府對PM2.5采用如下標準:
| PM2.5日均值m(微克/立方米) | 空氣質量等級 |
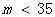 | 一級 |
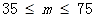 | 二級 |
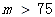 | 超標 |

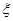 表示空氣質量達到一級的天數,求
表示空氣質量達到一級的天數,求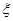 的分布列;
的分布列;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
深圳市某校中學生籃球隊假期集訓,集訓前共有6個籃球,其中3個是新球(即沒有用過的球),3個是舊球(即至少用過一次的球).每次訓練,都從中任意取出2個球,用完后放回.
(1)設第一次訓練時取到的新球個數為ξ,求ξ的分布列和數學期望;
(2)求第二次訓練時恰好取到一個新球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
哈六中體育節進行定點投籃游戲,已知參加游戲的甲、乙兩人,他們每一次投籃投中的概率均為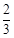 ,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.(12分)
,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.(12分)
(1)求甲同學至少有4次投中的概率;
(2)求乙同學投籃次數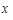 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為考察某種藥物預防禽流感的效果,進行動物家禽試驗,調查了100個樣本,統計結果為:服用藥的共有60個樣本,服用藥但患病的仍有20個樣本,沒有服用藥且未患病的有20個樣本.
(1)根據所給樣本數據完成下面2×2列聯表;
(2)請問能有多大把握認為藥物有效?
| | 不得禽流感 | 得禽流感 | 總計 |
| 服藥 | | | |
| 不服藥 | | | |
| 總計 | | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
地為綠化環境,移栽了銀杏樹 棵,梧桐樹
棵,梧桐樹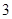 棵.它們移栽后的成活率分別
棵.它們移栽后的成活率分別
為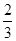 、
、 ,每棵樹是否存活互不影響,在移栽的
,每棵樹是否存活互不影響,在移栽的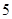 棵樹中:
棵樹中:
(1)求銀杏樹都成活且梧桐樹成活 棵的概率;
棵的概率;
(2)求成活的棵樹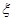 的分布列與期望.
的分布列與期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com