
【題目】如圖,四棱錐![]() ,底面
,底面![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.
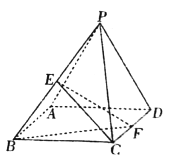
(1)求證![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)由題意,可取![]() 中點
中點![]() ,連接
,連接![]() ,則易知平面
,則易知平面![]() ∥平面
∥平面![]() ,由條件易證
,由條件易證![]() 平面
平面![]() ,則
,則![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,根據線面垂直的定義,從而問題可得證;(2)由題意,采用坐標法進行求解,可取
,根據線面垂直的定義,從而問題可得證;(2)由題意,采用坐標法進行求解,可取![]() 中點
中點![]() 為坐標原點,過
為坐標原點,過![]() 點作平行于
點作平行于![]() 的直線為
的直線為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,分別算出平面
軸,建立空間直角坐標系,分別算出平面![]() 和平面
和平面![]() 的法向量,結合圖形,二面角
的法向量,結合圖形,二面角![]() 為銳角,從而問題可得解.
為銳角,從而問題可得解.
試題解析:(1)取![]() 中點
中點![]() ,連結
,連結![]() ,
,![]() ,∵
,∵![]() 是正方形,∴
是正方形,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() 面
面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,
,![]() 都是中點,∴
都是中點,∴![]() ,
,![]() ,∴
,∴![]() 面
面![]() ,
,
∴![]() ;
;
(2)建立如圖空間直角坐標系,由題意得![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則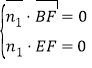 ,即
,即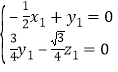 ,
,
令![]() ,則
,則![]() ,
,![]() ,得
,得![]() ,
,
同理得平面![]() 的法向量為
的法向量為![]() ,
,
∴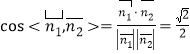 ,所以他的余弦值是
,所以他的余弦值是![]() .
.


科目:高中數學 來源: 題型:
【題目】某地某高中2018年的高考考生人數是2015年高考考生人數的1.5倍.為了更好地對比該校考生的升學情況,統計了該校2015和2018年高考情況,得到如下餅圖:

2018年與2015年比較,下列結論正確的是( )
A. 一本達線人數減少
B. 二本達線人數增加了0.5倍
C. 藝體達線人數相同
D. 不上線的人數有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數
,求實數![]() 的值;
的值;
(2)設![]() ,若對任意兩個不等的正數
,若對任意兩個不等的正數![]() ,
,![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.甲、乙兩人做游戲:甲、乙兩人各寫一個數字,若都是奇數或都是偶數則甲勝,否則乙勝,這個游戲公平
B.做![]() 次隨機試驗,事件
次隨機試驗,事件![]() 發生的頻率就是事件
發生的頻率就是事件![]() 發生的概率
發生的概率
C.某地發行福利彩票,回報率為47%,某人花了100元買該福利彩票,一定會有47元的回報
D.有甲、乙兩種報紙可供某人訂閱,事件![]() “某人訂閱甲報紙”是必然事件
“某人訂閱甲報紙”是必然事件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為D的函數f(x),若存在區間[m,n]![]() D,同時滿足下列條件:①f(x)在[m,n]上是單調的;②當定義域是[m,n]時,f(x)的值域也是[m,n],則稱[m,n]為該函數的“和諧區間”.下列函數存在“和諧區間”的有( )
D,同時滿足下列條件:①f(x)在[m,n]上是單調的;②當定義域是[m,n]時,f(x)的值域也是[m,n],則稱[m,n]為該函數的“和諧區間”.下列函數存在“和諧區間”的有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,動圓
中,動圓![]() 與圓
與圓![]() 外切,且圓
外切,且圓![]() 與直線
與直線![]() 相切,記動圓圓心
相切,記動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)設過定點![]() 的動直線
的動直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,試問:在曲線
兩點,試問:在曲線![]() 上是否存在點
上是否存在點![]() (與
(與![]() 兩點相異),當直線
兩點相異),當直線![]() 的斜率存在時,直線
的斜率存在時,直線![]() 的斜率之和為定值?若存在,求出點
的斜率之和為定值?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,直線
,直線![]() 與函數
與函數![]() 的圖象在
的圖象在![]() 處相切,設
處相切,設![]() ,若在區間[1,2]上,不等式
,若在區間[1,2]上,不等式![]() 恒成立.則實數m( )
恒成立.則實數m( )
A. 有最大值![]() B. 有最大值e C. 有最小值e D. 有最小值
B. 有最大值e C. 有最小值e D. 有最小值![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障全國第四次經濟普查順利進行,國家統計局從東部選擇江蘇,從中部選擇河北. 湖北,從西部選擇寧夏,從直轄市中選擇重慶作為國家綜合試點地區,然后再逐級確定普查區域,直到基層的普查小區.在普查過程中首先要進行宣傳培訓,然后確定對象,最后入戶登記.由于種種情況可能會導致入戶登記不夠順利,這為正式普查提供了寶貴的試點經驗.在某普查小區,共有 50 家企事業單位,150 家個體經營戶,普查情況如下表所示:
普查對象類別 | 順利 | 不順利 | 合計 |
企事業單位 | 40 | 50 | |
個體經營戶 | 50 | 150 | |
合計 |
(1)寫出選擇 5 個國家綜合試點地區采用的抽樣方法;
(2)補全上述列聯表(在答題卡填寫),并根據列聯表判斷是否有![]() 的把握認為“此普查小區的入戶登記是否順利與普查對象的類別有關”;
的把握認為“此普查小區的入戶登記是否順利與普查對象的類別有關”;
(3)根據該試點普查小區的情況,為保障第四次經濟普查的順利進行,請你從統計的角度提出一條建議.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果存在非零常數![]() ,對于函數
,對于函數![]() 定義域上的任意
定義域上的任意![]() ,都有
,都有![]() 成立,那么稱函數為“
成立,那么稱函數為“![]() 函數”.
函數”.
(Ⅰ)若![]() ,
,![]() ,試判斷函數
,試判斷函數![]() 和
和![]() 是否是“
是否是“![]() 函數”?若是,請證明:若不是,主說明理由:
函數”?若是,請證明:若不是,主說明理由:
(Ⅱ)求證:若![]() 是單調函數,則它是“
是單調函數,則它是“![]() 函數”;
函數”;
(Ⅲ)若函數![]() 是“
是“![]() 函數”,求實數
函數”,求實數![]() 滿足的條件.
滿足的條件.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com