
【題目】如圖,在平面直角坐標系xOy中,焦點在x軸上的橢圓C: ![]() =1經過點(b,2e),其中e為橢圓C的離心率.過點T(1,0)作斜率為k(k>0)的直線l交橢圓C于A,B兩點(A在x軸下方).
=1經過點(b,2e),其中e為橢圓C的離心率.過點T(1,0)作斜率為k(k>0)的直線l交橢圓C于A,B兩點(A在x軸下方).
(1)求橢圓C的標準方程;
(2)過點O且平行于l的直線交橢圓C于點M,N,求 ![]() 的值;
的值;
(3)記直線l與y軸的交點為P.若 ![]() =
= ![]()
![]() ,求直線l的斜率k.
,求直線l的斜率k.
【答案】
(1)
解:因為橢圓橢圓C: ![]() =1經過點(b,2e)所以
=1經過點(b,2e)所以 ![]() .
.
因為e2= ![]() ,所以
,所以 ![]() ,
,
又∵a2=b2+c2, ![]() ,解得b2=4或b2=8(舍去).
,解得b2=4或b2=8(舍去).
所以橢圓C的方程為 ![]()
(2)
解:設A(x1,y1),B(x2,y2).
因為T(1,0),則直線l的方程為y=k(x﹣1).
聯立直線l與橢圓方程 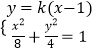 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
所以x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
因為MN∥l,所以直線MN方程為y=kx,
聯立直線MN與橢圓方程 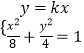
消去y得(2k2+1)x2=8,
解得x2= ![]()
因為MN∥l,所以 ![]()
因為(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]= ![]() .
.
(xM﹣xN)2=4x2= ![]() .
.
所以 ![]() =
= ![]()
(3)
解:在y=k(x﹣1)中,令x=0,則y=﹣k,所以P(0,﹣k),
從而 ![]() ,
,
∵ ![]() =
= ![]()
![]() ,
, ![]() …①
…①
由(2)知 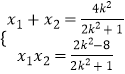 …②
…②
由①②得 ![]() 50k4﹣83k2﹣34=0,解得k2=2或k2=﹣
50k4﹣83k2﹣34=0,解得k2=2或k2=﹣ ![]() (舍).
(舍).
又因為k>0,所以k= ![]()
【解析】(1)由題意得e2= ![]() ,
, ![]() .又a2=b2+c2 ,
.又a2=b2+c2 , ![]() ,解得b2;(2)設A(x1 , y1),B(x2 , y2).設直線l的方程為y=k(x﹣1).
,解得b2;(2)設A(x1 , y1),B(x2 , y2).設直線l的方程為y=k(x﹣1).
聯立直線l與橢圓方程 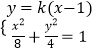 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可設直線MN方程為y=kx,聯立直線MN與橢圓方程
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可設直線MN方程為y=kx,聯立直線MN與橢圓方程 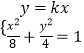 ,消去y得(2k2+1)x2=8,由MN∥l,得
,消去y得(2k2+1)x2=8,由MN∥l,得 ![]()
由(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]= ![]() .得(xM﹣xN)2=4x2=
.得(xM﹣xN)2=4x2= ![]() .即可. (3)在y=k(x﹣1)中,令x=0,則y=﹣k,所以P(0,﹣k),從而
.即可. (3)在y=k(x﹣1)中,令x=0,則y=﹣k,所以P(0,﹣k),從而 ![]() ,由
,由 ![]() =
= ![]()
![]() 得
得 ![]() …①,由(2)知
…①,由(2)知 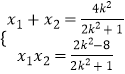 …②由①②得
…②由①②得 ![]() 50k4﹣83k2﹣34=0,解得k2
50k4﹣83k2﹣34=0,解得k2
【考點精析】認真審題,首先需要了解橢圓的標準方程(橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() ).
).


科目:高中數學 來源: 題型:
【題目】選修4﹣﹣4;坐標系與參數方程
已知動點P,Q都在曲線C: ![]() 上,對應參數分別為β=α與β=2α(0<α<2π),M為PQ的中點.
上,對應參數分別為β=α與β=2α(0<α<2π),M為PQ的中點.
(1)求M的軌跡的參數方程
(2)將M到坐標原點的距離d表示為α的函數,并判斷M的軌跡是否過坐標原點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自“釣魚島事件”以來,中日關系日趨緊張并不斷升級.為了積極響應“保釣行動”,某學校舉辦了一場“保釣知識大賽”,共分兩組.其中甲組得滿分的有1個女生和3個男生,乙組得滿分的有2個女生和4個男生.現從得滿分的同學中,每組各任選1個同學,作為“保釣行動代言人”.
(1)求選出的2個同學中恰有1個女生的概率;
(2)設X為選出的2個同學中女生的個數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生參加社會實踐活動,對某公司1月份至6月份銷售某種配件的銷售量及銷售單價進行了調查,銷售單價x和銷售量y之間的一組數據如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
銷售單價(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量(件) | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根據1至5月份的數據,求出y關于x的回歸直線方程;
(2)若由回歸直線方程得到的估計數據與剩下的檢驗數據的誤差不超過0.5元,則認為所得到的回歸直線方程是理想的,試問(1)中所得到的回歸直線方程是否理想?
(3)預計在今后的銷售中,銷售量與銷售單價仍然服從(1)中的關系,若該種機器配件的成本是2.5元/件,那么該配件的銷售單價應定為多少元才能獲得最大利潤?(注:利潤=銷售收入-成本).
參考公式:回歸直線方程![]() ,其中
,其中![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現要完成下列3項抽樣調查:
①從15種疫苗中抽取5種檢測是否合格.
②渦陽縣某中學共有480名教職工,其中一線教師360名,行政人員48名,后勤人員72名.為了解教職工對學校校務公開方面的意見,擬抽取一個容量為20的樣本.
③渦陽縣某中學報告廳有28排,每排有35個座位,一次報告會恰好坐滿了聽眾,報告會結束后,為了聽取意見,需要請28名聽眾進行座談.
較為合理的抽樣方法是( )
A. ①簡單隨機抽樣, ②系統抽樣, ③分層抽樣
B. ①簡單隨機抽樣, ②分層抽樣, ③系統抽樣
C. ①系統抽樣, ②簡單隨機抽樣, ③分層抽樣
D. ①分層抽樣, ②系統抽樣, ③簡單隨機抽樣
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,若存在實數
,若存在實數![]() ,使得對于任意的
,使得對于任意的![]() ,都有
,都有![]() ,則稱數列
,則稱數列![]() 為“
為“![]() 數列”( )
數列”( )
A. 若![]() 是等差數列,且首項
是等差數列,且首項![]() ,則數列
,則數列![]() 是“
是“![]() 數列”
數列”
B. 若![]() 是等差數列,且公差
是等差數列,且公差![]() ,則數列
,則數列![]() 是“
是“![]() 數列”
數列”
C. 若![]() 是等比數列,也是“
是等比數列,也是“![]() 數列”,則數列
數列”,則數列![]() 的公比
的公比![]() 滿足
滿足![]()
D. 若![]() 是等比數列,且公比
是等比數列,且公比![]() 滿足
滿足![]() ,則數列
,則數列![]() 是“
是“![]() 數列”
數列”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 數列{bn},{cn}滿足 (n+1)bn=an+1﹣ ![]() ,(n+2)cn=
,(n+2)cn= ![]() ﹣
﹣ ![]() ,其中n∈N*.
,其中n∈N*.
(1)若數列{an}是公差為2的等差數列,求數列{cn}的通項公式;
(2)若存在實數λ,使得對一切n∈N*,有bn≤λ≤cn , 求證:數列{an}是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某輿情機構為了解人們對某事件的關注度,隨機抽取了![]() 人進行調查,其中女性中對該事件關注的占
人進行調查,其中女性中對該事件關注的占![]() ,而男性有
,而男性有![]() 人表示對該事件沒有關注.
人表示對該事件沒有關注.
關注 | 沒關注 | 合計 | |
男 |
| ||
女 | |||
合計 |
(1)根據以上數據補全![]() 列聯表;
列聯表;
(2)能否有![]() 的把握認為“對事件是否關注與性別有關”?
的把握認為“對事件是否關注與性別有關”?
(3)已知在被調查的女性中有![]() 名大學生,這其中有
名大學生,這其中有![]() 名對此事關注.現在從這
名對此事關注.現在從這![]() 名女大學生中隨機抽取
名女大學生中隨機抽取![]() 人,求至少有
人,求至少有![]() 人對此事關注的概率.
人對此事關注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com