
【題目】已知在梯形![]() 中,
中, ![]() 平面
平面![]() ,且
,且![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,且
上,且![]() .
.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見(jiàn)解析(2)![]()
【解析】試題分析:(1)連接![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,利用平幾知識(shí)可得
,利用平幾知識(shí)可得![]() ,再根據(jù)相似比得
,再根據(jù)相似比得![]() .最后根據(jù)線面平行判定定理得
.最后根據(jù)線面平行判定定理得![]() 平面
平面![]() .(2)求二面角大小,一般利用空間向量數(shù)量積:先根據(jù)條件建立空間直角坐標(biāo)系,設(shè)立各點(diǎn)坐標(biāo),列方程組求各平面法向量,利用向量數(shù)量積求兩法向量夾角,最后根據(jù)二面角與法向量夾角關(guān)系求二面角.
.(2)求二面角大小,一般利用空間向量數(shù)量積:先根據(jù)條件建立空間直角坐標(biāo)系,設(shè)立各點(diǎn)坐標(biāo),列方程組求各平面法向量,利用向量數(shù)量積求兩法向量夾角,最后根據(jù)二面角與法向量夾角關(guān)系求二面角.
試題解析:解: (Ⅰ)連接![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,如圖①所示.
,如圖①所示.
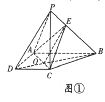
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)設(shè)![]() ∵
∵![]() 且
且![]() 平面
平面![]() ,故以
,故以![]() 為原點(diǎn),過(guò)點(diǎn)
為原點(diǎn),過(guò)點(diǎn)![]() 與
與![]() 平行的直線為
平行的直線為![]() 軸,
軸,
![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標(biāo)系如圖②所示,則
軸,建立空間直角坐標(biāo)系如圖②所示,則

![]() .
.
由![]() ,得
,得![]() ,得
,得![]() .
.
解得![]() ,即
,即![]() ,
,
![]() .
.
設(shè)![]() 是平面
是平面![]() 的一個(gè)法向量,則
的一個(gè)法向量,則![]()
令![]() ,則
,則![]() ,即
,即![]() .
.
取![]() 的中點(diǎn),記為
的中點(diǎn),記為![]() ,連接
,連接![]() ,
,
易求得![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
∴![]()
![]() .
.
由![]() ,得
,得![]() ,
,
由![]() 底面
底面![]() ,得
,得![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
∴![]() 是平面
是平面![]() 的一個(gè)法向量.
的一個(gè)法向量.
∴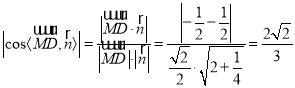 .
.
由圖可知二面角![]() 為銳二面角,
為銳二面角,
∴二面角![]() 的余弦值為
的余弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】PM2.5是指空氣中直徑小于或等于2.5微米的顆粒物(也稱可入肺顆粒物).為了探究車流量與PM2.5的濃度是否相關(guān),現(xiàn)采集到某城市周一至周五某一時(shí)間段車流量與PM2.5的數(shù)據(jù)如表:
時(shí)間 | 周一 | 周二 | 周三 | 周四 | 周五 |
車流量x(萬(wàn)輛) | 50 | 51 | 54 | 57 | 58 |
PM2.5的濃度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(1)根據(jù)上表數(shù)據(jù),請(qǐng)?jiān)谌鐖D坐標(biāo)系中畫出散點(diǎn)圖; 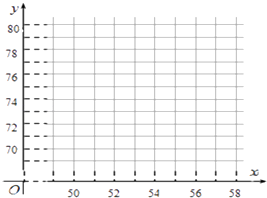
(2)根據(jù)上表數(shù)據(jù),用最小二乘法求出y關(guān)于x的線性回歸方程 ![]() ;(保留2位小數(shù))
;(保留2位小數(shù))
(3)若周六同一時(shí)間段車流量是25萬(wàn)輛,試根據(jù)(2)求出的線性回歸方程預(yù)測(cè),此時(shí)PM2.5的濃度為多少(保留整數(shù))?
參考公式: ![]() =
= 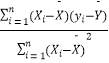 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】五一節(jié)期間,某商場(chǎng)為吸引顧客消費(fèi)推出一項(xiàng)優(yōu)惠活動(dòng),活動(dòng)規(guī)則如下:消費(fèi)額每滿100元可轉(zhuǎn)動(dòng)如圖所示的轉(zhuǎn)盤一次,并獲得相應(yīng)金額的返券.(假定指針等可能地停在任一位置,指針落在區(qū)域的邊界時(shí),重新轉(zhuǎn)一次)指針?biāo)诘膮^(qū)域及對(duì)應(yīng)的返劵金額見(jiàn)表.
例如:消費(fèi)218元,可轉(zhuǎn)動(dòng)轉(zhuǎn)盤2次,所獲得的返券金額是兩次金額之和.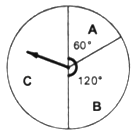
(1)已知顧客甲消費(fèi)后獲得n次轉(zhuǎn)動(dòng)轉(zhuǎn)盤的機(jī)會(huì),已知他每轉(zhuǎn)一次轉(zhuǎn)盤指針落在區(qū)域邊界的概率為p,每次轉(zhuǎn)動(dòng)轉(zhuǎn)盤的結(jié)果相互獨(dú)立,設(shè)ξ為顧客甲轉(zhuǎn)動(dòng)轉(zhuǎn)盤指針落在區(qū)域邊界的次數(shù),ξ的數(shù)學(xué)期望Eξ= ![]() ,方差Dξ=
,方差Dξ= ![]() ,求n、p的值;
,求n、p的值;
(2)顧客乙消費(fèi)280元,并按規(guī)則參與了活動(dòng),他獲得返券的金額記為η(元).求隨機(jī)變量η的分布列和數(shù)學(xué)期望.
指針位置 | A區(qū)域 | B區(qū)域 | C區(qū)域 |
返券金額(單位:元) | 60 | 30 | 0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ![]() ,1)上是減函數(shù),求a的取值范圍.
,1)上是減函數(shù),求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知整數(shù)對(duì)按如圖規(guī)律排成,照此規(guī)律,則第68個(gè)數(shù)對(duì)是 . 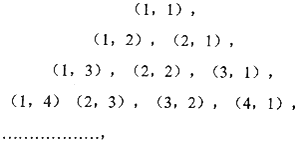
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn), ![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,圓
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點(diǎn).
兩點(diǎn).
(1)求圓![]() 的直角坐標(biāo)方程及弦
的直角坐標(biāo)方程及弦![]() 的長(zhǎng);
的長(zhǎng);
(2)動(dòng)點(diǎn)![]() 在圓
在圓![]() 上(不與
上(不與![]() ,
, ![]() 重合),試求
重合),試求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn), ![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,圓
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點(diǎn).
兩點(diǎn).
(1)求圓![]() 的直角坐標(biāo)方程及弦
的直角坐標(biāo)方程及弦![]() 的長(zhǎng);
的長(zhǎng);
(2)動(dòng)點(diǎn)![]() 在圓
在圓![]() 上(不與
上(不與![]() ,
, ![]() 重合),試求
重合),試求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義域?yàn)镽的函數(shù)f(x)滿足f(x+2)=2f(x),當(dāng)x∈[0,2)時(shí),f(x)= 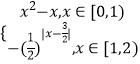 ,若x∈[﹣4,﹣2)時(shí),f(x)≥
,若x∈[﹣4,﹣2)時(shí),f(x)≥ ![]() 恒成立,則實(shí)數(shù)t的取值范圍是( )
恒成立,則實(shí)數(shù)t的取值范圍是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1]
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com