
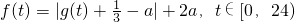 ,其中,
,其中,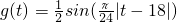 代表大氣中某類隨時間t變化的典型污染物質的含量;參數a代表某個已測定的環境氣象指標,且
代表大氣中某類隨時間t變化的典型污染物質的含量;參數a代表某個已測定的環境氣象指標,且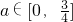 .
. |t-18|∈[
|t-18|∈[ ,
,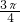 ],
], ];
]; ],f(t)的最大值M(a),
],f(t)的最大值M(a), ]時,M(a)=|
]時,M(a)=| +
+ -a|+2a=a+
-a|+2a=a+ ;
; ,
, ]時,M(a)=|
]時,M(a)=| -a|+2a=3a-
-a|+2a=3a- .
.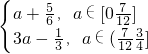 ;
;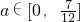 時,M(a)=
時,M(a)=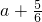 ≤
≤ +
+ =
=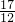 <2;
<2;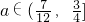 時,M(a)=
時,M(a)= ≤
≤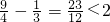 .
. |t-18|的范圍,然后結合三角函數的性質求出g(t)的值域;
|t-18|的范圍,然后結合三角函數的性質求出g(t)的值域; ]和(
]和( ,
, ]上討論絕對值的取值得到M(a)的解析式為分段函數;
]上討論絕對值的取值得到M(a)的解析式為分段函數;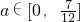 時和
時和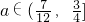 時分別討論M(a)的最值與2的關系即可.
時分別討論M(a)的最值與2的關系即可.

 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 24 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2008年上海市普陀區高考數學一模試卷(解析版) 題型:解答題
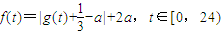 ,其中,
,其中,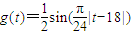 代表大氣中某類隨時間t變化的典型污染物質的含量;參數a代表某個已測定的環境氣象指標,且
代表大氣中某類隨時間t變化的典型污染物質的含量;參數a代表某個已測定的環境氣象指標,且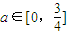 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com