
【題目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),函數f(x)=
),函數f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1,x∈[﹣
|+1,x∈[﹣ ![]() ,
, ![]() ],m∈R.
],m∈R.
(1)當m=0時,求f( ![]() )的值;
)的值;
(2)若f(x)的最小值為﹣1,求實數m的值;
(3)是否存在實數m,使函數g(x)=f(x)+ ![]() m2 , x∈[﹣
m2 , x∈[﹣ ![]() ,
, ![]() ]有四個不同的零點?若存在,求出m的取值范圍;若不存在,說明理由.
]有四個不同的零點?若存在,求出m的取值范圍;若不存在,說明理由.
【答案】
(1)解: ![]()
![]() =(cos
=(cos ![]() ,sin
,sin ![]() )(cos
)(cos ![]() ,﹣sin
,﹣sin ![]() )=cos
)=cos ![]() cos
cos ![]() ﹣sin
﹣sin ![]() sin
sin ![]() =cos(
=cos( ![]() +
+ ![]() )=cos2x,
)=cos2x,
當m=0時,f(x)= ![]()
![]() +1=cos2x+1,
+1=cos2x+1,
則f( ![]() )=cos(2×
)=cos(2× ![]() )+1=cos
)+1=cos ![]() +1=
+1= ![]()
(2)解:∵x∈[﹣ ![]() ,
, ![]() ],
],
∴| ![]() +
+ ![]() |=
|= ![]() =
= ![]() =2cosx,
=2cosx,
則f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
令t=cosx,則 ![]() ≤t≤1,
≤t≤1,
則y=2t2﹣2mt,對稱軸t= ![]() ,
,
① 當 ![]() <
< ![]() ,即m<1時,
,即m<1時,
當t= ![]() 時,函數取得最小值此時最小值y=
時,函數取得最小值此時最小值y= ![]() ﹣m=﹣1,得m=
﹣m=﹣1,得m= ![]() (舍),
(舍),
②當 ![]() ≤
≤ ![]() ≤1,即m<1時,
≤1,即m<1時,
當t= ![]() 時,函數取得最小值此時最小值y=﹣
時,函數取得最小值此時最小值y=﹣ ![]() =﹣1,得m=
=﹣1,得m= ![]() ,
,
③當 ![]() >1,即m>2時,
>1,即m>2時,
當t=1時,函數取得最小值此時最小值y=2﹣2m=﹣1,得m= ![]() (舍),
(舍),
綜上若f(x)的最小值為﹣1,則實數m= ![]()
(3)解:令g(x)=2cos2x﹣2mcosx+ ![]() m2=0,得cosx=
m2=0,得cosx= ![]() 或
或 ![]() ,
,
∴方程cosx= ![]() 或
或 ![]() 在x∈[﹣
在x∈[﹣ ![]() ,
, ![]() ]上有四個不同的實根,
]上有四個不同的實根,
則 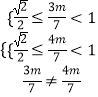 ,得
,得 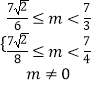 ,則
,則 ![]() ≤m<
≤m< ![]() ,
,
即實數m的取值范圍是 ![]() ≤m<
≤m< ![]()
【解析】(1)利用向量數量積的公式化簡函數f(x)即可.(2)求出函數f(x)的表達式,利用換元法結合一元二次函數的最值性質進行討論求解即可.(3)由g(x)=0得到方程的根,利用三角函數的性質進行求解即可.


 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】蘭州一中在世界讀書日期間開展了“書香校園”系列讀書教育活動。為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調查。下面是根據調查結果繪制的學生日均課外閱讀時間(單位:分鐘)的頻率分布直方圖,且將日均課外閱讀時間不低于60分鐘的學生稱為“讀書迷”,低于60分鐘的學生稱為“非讀書迷”。
非讀書迷 | 讀書迷 | 合計 | |
男 | 15 | ||
女 | 45 |
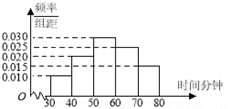
(1)根據已知條件完成下面2×2列聯表,并據此判斷是否有99%的把握認為“讀書迷”與性別有關?
(2)利用分層抽樣從這100名學生的“讀書迷”中抽取8名進行集訓,從中選派2名參加蘭州市讀書知識比賽,求至少有一名男生參加比賽的概率。
附: 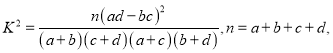
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 過橢圓
過橢圓![]() :
: ![]() (
(![]() )的短軸端點,
)的短軸端點, ![]() ,
, ![]() 分別是圓
分別是圓![]() 與橢圓
與橢圓![]() 上任意兩點,且線段
上任意兩點,且線段![]() 長度的最大值為3.
長度的最大值為3.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作圓
作圓![]() 的一條切線交橢圓
的一條切線交橢圓![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,四邊形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H為BC的中點.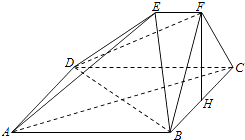
(1)求證:FH∥平面EDB;
(2)求證:AC⊥平面EDB;
(3)解:求二面角B﹣DE﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)若f(x)在( ![]() ,+∞)上是單調減函數,求實數a的取值范圍.
,+∞)上是單調減函數,求實數a的取值范圍.
(2)當0<a<2時,f(x)在[1,4]上的最小值為﹣ ![]() ,求f(x)在該區間的最大值.
,求f(x)在該區間的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)═log2( ![]() +a).
+a).
(1)若f(1)<2,求實數a的取值范圍;
(2)設函數g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5],討論函數g(x)的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() ,橢圓
,橢圓![]() ,
, ![]() 為橢圓
為橢圓![]() 的右頂點,過原點且異于
的右頂點,過原點且異于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 交于
交于![]() 兩點,
兩點, ![]() 在
在![]() 軸的上方,直線
軸的上方,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,直線
,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,
,
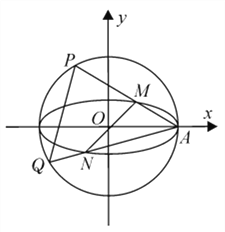
(1)若![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)設![]() 與
與![]() 的面積分別為
的面積分別為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com