【題目】設(shè)函數(shù)
.
（1）求函數(shù)
的極小值；
（2）證明：當(dāng)
時，不等式
恒成立.
【答案】（1）0；（2）見解析.
【解析】
（1）對函數(shù)
求導(dǎo)，分析函數(shù)的單調(diào)性，即可求出極小值；
（2）方法一：不等式
恒成立等價于
恒成立. 令
，對函數(shù)
求導(dǎo)，分析函數(shù)的單調(diào)性，即可證明. 方法二：令
.通過對函數(shù)二次求導(dǎo)，分析函數(shù)的單調(diào)性，即可證明.
（1）
，
則
，令
，則
.
當(dāng)
時，
，為單調(diào)遞減函數(shù)；當(dāng)
時，
，
為單調(diào)增函數(shù)；所以當(dāng)時，函數(shù)取得極小值
.
（2）方法一：
當(dāng)
時，不等式恒成立
等價于恒成立.
令，
則
.
所以，當(dāng)
時，
，
所以，在
上單調(diào)遞增.
，
所以.
即當(dāng)
時，恒成立.
方法二：當(dāng)時，不等式恒成立
等價于
恒成立，
即
恒成立，
令，
則
.
令
，
則
.
因為，所以
，
所以
在上單調(diào)遞增，所以
，
故在上單調(diào)遞增，
所以，
即.
所以，當(dāng)時，不等式成立.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某手機廠商在銷售200萬臺某型號手機時開展“手機碎屏險”活動、活動規(guī)則如下：用戶購買該型號手機時可選購“手機碎屏險”，保費為
元，若在購機后一年內(nèi)發(fā)生碎屏可免費更換一次屏幕．該手機廠商將在這
萬臺該型號手機全部銷售完畢一年后，在購買碎屏險且購機后一年內(nèi)未發(fā)生碎屏的用戶中隨機抽取
名，每名用戶贈送元的紅包，為了合理確定保費的值，該手機廠商進(jìn)行了問卷調(diào)查，統(tǒng)計后得到下表（其中
表示保費為元時愿意購買該“手機碎屏險”的用戶比例）；
（1）根據(jù)上面的數(shù)據(jù)求出關(guān)于的回歸直線方程；
（2）通過大數(shù)據(jù)分析，在使用該型號手機的用戶中，購機后一年內(nèi)發(fā)生碎屏的比例為
．已知更換一次該型號手機屏幕的費用為
元，若該手機廠商要求在這次活動中因銷售該“手機碎屏險”產(chǎn)生的利潤不少于
萬元，能否把保費定為5元？
x | 10 | 20 | 30 | 40 | 50 |
y | 0.79 | 0.59 | 0.38 | 0.23 | 0.01 |
參考公式：回歸方程
中斜率和截距的最小二乘估計分別為
，
，
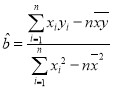參考數(shù)據(jù)：表中的5個值從左到右分別記為
，相應(yīng)的值分別記為
，經(jīng)計算有
，其中
，
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在四棱錐P–ABCD中，
，
．
（1）設(shè)AC與BD相交于點M，
，且
平面PCD，求實數(shù)m的值；
（2）若
，
，
，且
，求二面角
的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)橢圓
的右焦點為
，過點
作直線
與橢圓
交于
，
兩點，且坐標(biāo)原點
到直線的距離為1．
（1）當(dāng)
時，求直線
的方程；
（2）求
面積的最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）＝|sinx||cosx|，則下列說法正確的是（ ）
A.f（x）的圖象關(guān)于直線
對稱
B.f（x）的周期為
C.（π，0）是f（x）的一個對稱中心
D.f（x）在區(qū)間
上單調(diào)遞增
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為更好地落實農(nóng)民工工資保證金制度，南方某市勞動保障部門調(diào)查了
年下半年該市
名農(nóng)民工（其中技術(shù)工、非技術(shù)工各
名）的月工資，得到這名農(nóng)民工月工資的中位數(shù)為
百元（假設(shè)這名農(nóng)民工的月工資均在
（百元）內(nèi)）且月工資收入在
（百元）內(nèi)的人數(shù)為
，并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖：
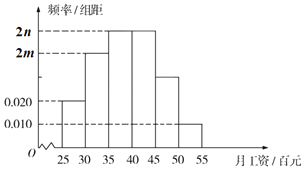
（Ⅰ）求
，
的值；
（Ⅱ）已知這名農(nóng)民工中月工資高于平均數(shù)的技術(shù)工有
名，非技術(shù)工有
名，則能否在犯錯誤的概率不超過
的前提下認(rèn)為是不是技術(shù)工與月工資是否高于平均數(shù)有關(guān)系？
參考公式及數(shù)據(jù)：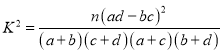
，其中
．
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知定義在
上的連續(xù)函數(shù)
對任意實數(shù)
滿足
，
，則下列命題正確的有________.
①若
，則函數(shù)有兩個零點；
②函數(shù)
為偶函數(shù)；
③
；
④若
且
,則
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
