【題目】(2017·北京高考)由四棱柱ABCDA1B1C1D1截去三棱錐C1B1CD1后得到的幾何體如圖所示．四邊形ABCD為正方形，O為AC與BD的交點，E為AD的中點，A1E⊥平面ABCD.
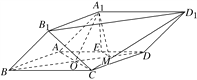
(1)證明：A1O∥平面B1CD1；
(2)設M是OD的中點，證明：平面A1EM⊥平面B1CD1.
科目：高中數學 來源： 題型：
【題目】定義：如果函數f（x）在[a，b]上存在x1 ， x2（a＜x1＜x2＜b）滿足 
， 
，則稱函數f（x）是[a，b]上的“雙中值函數”．已知函數f（x）=x3﹣x2+a是[0，a]上的“雙中值函數”，則實數a的取值范圍是（ ）
A.
B.（ 
）
C.（ 
，1）
D.（ 
，1）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓 
=1（a＞b＞0），F1、F2分別為橢 圓的左、右焦點，A為橢圓的上頂點，直線AF2交橢圓于另一點B、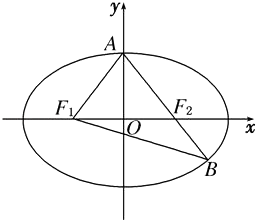
（1）若∠F1AB=90°，求橢圓的離心率；
（2）若 
=2 
， 
= 
，求橢圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知四邊形ABCD和BCEG均為直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=90°，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG.
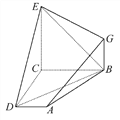
(1)求證：EC⊥CD.
(2)求證：AG∥平面BDE.
查看答案和解析>>
科目：高中數學 來源： 題型：
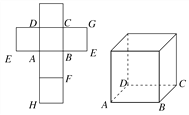
【題目】一個正方體的平面展開圖及該正方體的直觀圖的示意圖如圖所示.
(1)請按字母F、G、H標記在正方體相應地頂點處(不需要說明理由)；
(2)判斷平面BEG與平面ACH的位置關系．并說明你的結論；
(3)證明：直線DF⊥平面BEG.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某食品的保鮮時間t（單位：小時）與儲藏溫度x（單位：℃）滿足函數關系t=
且該食品在4℃的保鮮時間是16小時。已知甲在某日上午10時購買了該食品，并將其遺放在室外，且此日的室外溫度隨時間變化如圖所示。給出以下四個結論：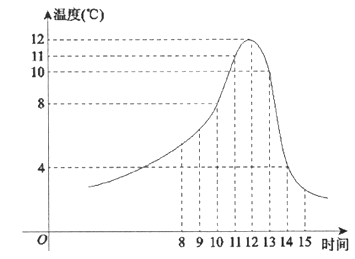
①該食品在6℃的保鮮時間是8小時；
②當x∈[-6，6]時，該食品的保鮮時間t隨著x增大而逐漸減少；
③到了此日13時，甲所購買的食品還在保鮮時間內；
④到了此日14時，甲所購買的食品已然過了保鮮時間。
其中，所有正確結論的序號是__________。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
