
【題目】已知向量![]() ,函數
,函數![]() ,
,
![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)若![]() 的最小值為
的最小值為![]() ,求實數
,求實數![]() 的值;
的值;
(3)是否存在實數![]() ,使函數
,使函數![]() ,
,![]() 有四個不同的零點?若存在,求出
有四個不同的零點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在實數m滿足條件,且其范圍為
;(3)存在實數m滿足條件,且其范圍為![]() 。
。
【解析】
(1)首先由平面向量數量積的坐標運算求得函數![]() 的解析式,然后求解
的解析式,然后求解![]() 時
時![]() 的值即可;
的值即可;
(2)由題意可得![]() 2cos2x﹣2mcosx,換元后結合二次函數的性質分類討論求解實數
2cos2x﹣2mcosx,換元后結合二次函數的性質分類討論求解實數![]() 的值即可;
的值即可;
(3)令![]() 求解
求解![]() 的值,據此求得關于
的值,據此求得關于![]() 的不等式,求解不等式可得實數m的取值范圍是
的不等式,求解不等式可得實數m的取值范圍是![]() .
.
(1)![]()
![]() =(cos
=(cos![]() ,sin
,sin![]() )(cos
)(cos![]() ,﹣sin
,﹣sin![]() )
)
=cos![]() cos
cos![]() ﹣sin
﹣sin![]() sin
sin![]() =cos(
=cos(![]() +
+![]() )=cos2x,
)=cos2x,
當m=0時,f(x)=![]()
![]() +1=cos2x+1,
+1=cos2x+1,
則f(![]() )=cos(2×
)=cos(2×![]() )+1=cos
)+1=cos![]() +1=
+1=![]() ;
;
(2)∵x∈[﹣![]() ,
,![]() ],
],
∴|![]() +
+![]() |=
|=![]() =
=![]() =2cosx,
=2cosx,
則f(x)=![]()
![]() ﹣m|
﹣m|![]() +
+![]() |+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
令t=cosx,則![]() ≤t≤1, 則y=2t2﹣2mt,對稱軸t=
≤t≤1, 則y=2t2﹣2mt,對稱軸t=![]() ,
,
①當![]() <
<![]() ,即m<1時,
,即m<1時,
當t=![]() 時,函數取得最小值此時最小值y=
時,函數取得最小值此時最小值y=![]() ﹣m=﹣1,得m=
﹣m=﹣1,得m=![]() (舍),
(舍),
②當![]() ≤
≤![]() ≤1,即m<1時,
≤1,即m<1時,
當t=![]() 時,函數取得最小值此時最小值y=﹣
時,函數取得最小值此時最小值y=﹣![]() =﹣1,得m=
=﹣1,得m=![]() ,
,
③當![]() >1,即m>2時,
>1,即m>2時,
當t=1時,函數取得最小值此時最小值y=2﹣2m=﹣1,得m=![]() (舍),
(舍),
綜上若f(x)的最小值為﹣1,則實數![]() .
.
(3)令g(x)=2cos2x﹣2mcosx+![]() m2=0,得cosx=
m2=0,得cosx=![]() 或cosx=
或cosx=![]() ,
,
∴方程cosx=![]() 或
或![]() 在x∈[﹣
在x∈[﹣![]() ,
,![]() ]上有四個不同的實根,
]上有四個不同的實根,
則 ,得
,得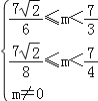 ,則
,則![]() ≤m<
≤m<![]() ,
,
即實數m的取值范圍是![]() .
.


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:高中數學 來源: 題型:
【題目】如圖,在平行六面體ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ![]() ,∠BAD=120°.
,∠BAD=120°.
(Ⅰ)求異面直線A1B與AC1所成角的余弦值;
(Ⅱ)求二面角B﹣A1D﹣A的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() .
.
(1)若直線不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 交
交![]() 軸負半軸于
軸負半軸于![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,求
,求![]() 的面積的最小值并求此時直線
的面積的最小值并求此時直線![]() 的方程;
的方程;
(3)已知點![]() ,若點
,若點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的最大值并求此時直線
的最大值并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() (
(![]() )的一個焦點,過原點的直線
)的一個焦點,過原點的直線![]() 與橢圓交于
與橢圓交于![]() 、
、![]() 兩點,且
兩點,且![]() ,△
,△![]() 的面積為
的面積為![]() 。
。
(1)求橢圓的離心率;
(2)若![]() ,過點
,過點![]() 且不與坐標軸垂直的直線交橢圓于
且不與坐標軸垂直的直線交橢圓于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,求點
,求點![]() 橫坐標的取值范圍。
橫坐標的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分)
(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,且四棱錐P﹣ABCD的體積為 ![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程選講]
在直角坐標系xOy中,曲線C的參數方程為 ![]() (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為 ![]() (t為參數).(10分)
(t為參數).(10分)
(1)若a=﹣1,求C與l的交點坐標;
(2)若C上的點到l距離的最大值為 ![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第47條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”, 《中華人民共和國道路交通安全法》第90條規定:對不禮讓行人的駕駛員處以扣3分,罰款50元的處罰.下表是某市一主干路口監控設備所抓拍的5個月內駕駛員“禮讓斑馬線”行為統計數據:
月份 | 1 | 2 | 3 | 4 | 5 |
違章駕駛員人數 | 120 | 105 | 100 | 90 | 85 |
(1)請利用所給數據求違章人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ;
;
(2)預測該路口9月份的不“禮讓斑馬線”違章駕駛員人數.
參考公式:  ,
, ![]() .
.
參考數據: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com