【題目】若函數
在區間
內恰有2019個零點，則
________
【答案】
【解析】
根據零點的定義可知，方程
，即
在
內有有2019個根，顯然
不滿足方程，所以
令
，再研究直線
與函數
的交點個數，即可解出．
令，即有，因為不滿足方程，所以，令
，∴
．∵函數在
上遞增，在
上遞增，由圖象可知，直線與函數的圖象至少有一個交點．
當
時，直線與函數的圖象只有一個交點，此時
，在一個周期
內的
上有兩個解，所以在區間
內不可能有奇數個解；
當
時，同理可得，在區間內不可能有奇數個解；
當
時，直線與函數的圖象有兩個交點，一個
，一個
，所以在一個周期內，
有兩個解，有兩個解，所以在區間內不可能有奇數個解；
當
時，直線與函數的圖象有兩個交點，一個
，一個
，所以在一個周期內，有兩個解，有一個解，即一個周期內有三個解，所以
，即
．
當
時，同理可得，
．
故答案為：．
科目：高中數學 來源： 題型：
【題目】某人在塔的正東方向沿著南偏西60°的方向前進40 m以后，望見塔在東北方向上，若沿途測得塔的最大仰角為30°，則塔高為________________m．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某網站舉行“衛生防疫”的知識競賽網上答題，共有120000人通過該網站參加了這次競賽，為了解競賽成績情況，從中抽取了100人的成績進行統計，其中成績分組區間為
，
，
，
，
，其頻率分布直方圖如圖所示，請你解答下列問題：
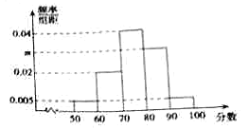
（1）求
的值；
（2）成績不低于90分的人就能獲得積分獎勵，求所有參賽者中獲得獎勵的人數；
（3）根據頻率分布直方圖，估計這次知識競賽成績的平均分（用組中值代替各組數據的平均值）.
查看答案和解析>>
科目：高中數學 來源： 題型：
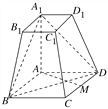
【題目】如圖所示，在四棱臺ABCDA1B1C1D1中，AA1⊥底面ABCD，四邊形ABCD為菱形，∠BAD＝120°，AB＝AA1＝2A1B1＝2.
(1)若M為CD中點，求證：AM⊥平面AA1B1B；
(2)求直線DD1與平面A1BD所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖①，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AD＝CD＝
AB＝2.將△ADC沿AC折起，使平面ADC⊥平面ABC，得到幾何體DABC，如圖②所示．
(1)證明：平面ABD⊥平面BCD；
(2)求二面角DABC的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若數列
共有k
項，且同時滿足
，
，則稱數列為
數列.
（1）若等比數列為
數列，求
的值；
（2）已知
為給定的正整數，且
，
①若公差為
的等差數列是
數列，求公差d；
②若數列
的通項公式為
，其中常數
，判斷數列是否為
數列，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某海濱城市附近海面有一臺風，據監測，當前臺風中心位于城市
（如圖）的東偏南
方向300千米的海面
處，并以20千米/時的速度向西偏北45°方向移動，臺風侵襲的范圍為圓形區域，當前半徑為60千米，并以10千米/時的速度不斷增大，問幾個小時后該城市開始受到臺風的侵襲？受到臺風的侵襲的時間有多少小時？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知直線
過點
，且傾斜角為
，以坐標原點為極點， 
軸的正半軸為極軸建立極坐標系，圓
的極坐標方程為
．
（1）求圓
的直角坐標方程及直線
的參數方程；
（2）設直線
與圓
的兩個交點分別為
， 
，求證：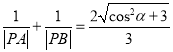 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
，其中
為自然對數的底數.
（Ⅰ）求曲線
在點
處的切線方程；
（Ⅱ）若對任意
，不等式
恒成立，求實數
的取值范圍；
（Ⅲ）試探究當
時，方程
的解的個數，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com