
【題目】在某公司的職工食堂中,食堂每天以3元/個的價格從面包店購進(jìn)面包,然后以5元/個的價格出售.如果當(dāng)天賣不完,剩下的面包以1元/個的價格賣給飼料加工廠.根據(jù)以往統(tǒng)計資料,得到食堂每天面包需求量的頻率分布直方圖如圖所示.食堂某天購進(jìn)了 90個面包,以![]() (個)(其中
(個)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利潤.
(元)表示利潤.
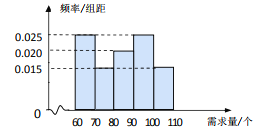
(1)根據(jù)直方圖計算需求量的中位數(shù);
(2)估計利潤![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方圖的需求量分組中,以需求量落入該區(qū)間的頻率作為需求量在該區(qū)間的概率,求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
【答案】(1)85個;(2) ![]() ;(3)142.
;(3)142.
【解析】試題分析:(1)需求量的中位數(shù)![]() (個)
(個)
(2)由題意可得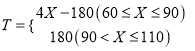 .
.
設(shè)利潤![]() 不少于100元為事件
不少于100元為事件![]() ,利潤
,利潤![]() 不少于100元時, 可得
不少于100元時, 可得![]() ,即
,即![]() ,由直方圖可知,由此可估計當(dāng)
,由直方圖可知,由此可估計當(dāng)![]() 時的概率.
時的概率.
(3)由題意,可得利潤![]() 的取值可為:80,120,160,180,分別求得
的取值可為:80,120,160,180,分別求得
![]() ,得到利潤
,得到利潤![]() 的分布列,則
的分布列,則![]() 的數(shù)學(xué)期望可求.
的數(shù)學(xué)期望可求.
試題解析:(1)需求量的中位數(shù)![]() (個)(其它解法也給分)
(個)(其它解法也給分)
(2)由題意,當(dāng)![]() 時,利潤
時,利潤![]() ,
,
當(dāng)![]() 時,利潤
時,利潤![]() ,
,
即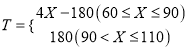 .
.
設(shè)利潤![]() 不少于100元為事件
不少于100元為事件![]() ,利潤
,利潤![]() 不少于100元時,即
不少于100元時,即![]() ,
,
∴![]() ,即
,即![]() ,由直方圖可知,當(dāng)
,由直方圖可知,當(dāng)![]() 時,
時,
所求概率: ![]()
(3)由題意,由于![]() ,
,
故利潤![]() 的取值可為:80,120,160,180,
的取值可為:80,120,160,180,
且![]() ,
,
故得分布列為:
![]()
利潤的數(shù)學(xué)期望![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2sin (2x+ ![]() ).
).
(1)求函數(shù)f(x)的最小正周期及其單調(diào)減區(qū)間;
(2)用“五點(diǎn)法”畫出函數(shù)g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的圖象(完成列表格并作圖),由圖象研究并寫出g(x)的對稱軸和對稱中心.
]的圖象(完成列表格并作圖),由圖象研究并寫出g(x)的對稱軸和對稱中心.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當(dāng)![]() 時,解不等式
時,解不等式![]() ;
;
(2)設(shè)![]() ,若對任意
,若對任意![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等差數(shù)列![]() 滿足
滿足![]() ,
, ![]() .
.
(![]() )求
)求![]() 的通項(xiàng)公式.
的通項(xiàng)公式.
(![]() )設(shè)等比數(shù)列
)設(shè)等比數(shù)列![]() 滿足
滿足![]() ,
, ![]() ,問:
,問: ![]() 與數(shù)列
與數(shù)列![]() 的第幾項(xiàng)相等?
的第幾項(xiàng)相等?
(![]() )試比較
)試比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某社區(qū)為豐富居民節(jié)日活動,組織了“迎新春”象棋大賽,已知報名的選手情況統(tǒng)計如下表:
組別 | 男 | 女 | 總計 |
中年組 |
|
| 91 |
老年組 | 16 |
|
|
已知中年組女性選手人數(shù)是僅比老年組女性選手人數(shù)多2人,若對中年組和老年組分別利用分層抽樣的方法抽取部分報名者參加比賽,已知老年組抽取了5人,其中女性3人,中年組抽取了7人.
(1)求表格中的數(shù)據(jù)![]() ;
;
(2)若從選出的中年組的選手中隨機(jī)抽取兩名進(jìn)行比賽,求至少有一名女性選手的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知正三棱柱ABC=A1B1C1的各棱長都是4,E是BC的中點(diǎn),動點(diǎn)F在側(cè)棱CC1上,且不與點(diǎn)C重合.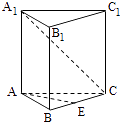
(1)當(dāng)CF=1時,求證:EF⊥A1C;
(2)設(shè)二面角C﹣AF﹣E的大小為θ,求tanθ的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足對任意的
滿足對任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)數(shù)列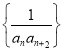 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,不等式
,不等式![]() 對任意的正整數(shù)
對任意的正整數(shù)![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 過點(diǎn)
過點(diǎn)![]() ,其離心率為
,其離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 相交于
相交于![]() 兩點(diǎn),在
兩點(diǎn),在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使
,使![]() 為正三角形,若存在,求直線
為正三角形,若存在,求直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列判斷正確的是 . (填寫所有正確的序號) ①若sinx+siny= ![]() ,則siny﹣cos2x的最大值為
,則siny﹣cos2x的最大值為 ![]() ;
;
②函數(shù)y=sin(2x+ ![]() )的單調(diào)增區(qū)間是[kπ﹣
)的單調(diào)增區(qū)間是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
③函數(shù)f(x)= ![]() 是奇函數(shù);
是奇函數(shù);
④函數(shù)y=tan ![]() ﹣
﹣ ![]() 的最小正周期是π.
的最小正周期是π.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com