【題目】函數f（x）= 
的定義域為（ ）
A.[0，1）
B.[0，2）
C.（1，2）
D.[0，1）∪（1，2）
科目：高中數學 來源： 題型：
【題目】已知A={x| 
＜3x＜9}，B={x|log2x＞0}．
（1）求A∩B和A∪B；
（2）定義A﹣B={x|x∈A且xB}，求A﹣B和B﹣A．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，已知點
，曲線
的參數方程為
（
為參數）．以原點為極點， 
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
．
（Ⅰ）判斷點
與直線
的位置關系并說明理由；
（Ⅱ）設直線
與曲線
的兩個交點分別為
， 
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數g（x）=3x ， h（x）=9x ．
（1）解方程：h（x）﹣8g（x）﹣h（1）=0；
（2）令p（x）= 
，求值：p（ 
）+p（ 
）+…+p（ 
）+p（ 
）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）是定義在R上的偶函數，且當x≤0時，f（x）=x2+2x．現已畫出函數f（x）在y軸左側的圖象，如圖所示，并根據 
（1）寫出函數f（x）（x∈R）的增區間；
（2）寫出函數f（x）（x∈R）的解析式；
（3）若函數g（x）=f（x）﹣2ax+2（x∈[1，2]），求函數g（x）的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為了解高一學生周末的“閱讀時間”，從高一年級中隨機抽取了
名學生進行調査，獲得了每人的周末“閱讀時間”（單位：小時），按照
分成
組，制成樣本的頻率分布直方圖如圖所示：
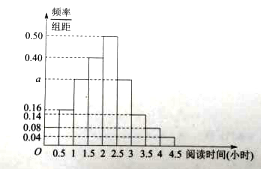
（Ⅰ）求圖中
的值；
（Ⅱ）估計該校高一學生周末“閱讀時間”的中位數；
（Ⅲ）用樣本頻率代替概率. 現從全校高一年級隨機抽取
名學生，其中有
名學生“閱讀時間”在
小時內的概率為
，其中
.當
取最大時，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列四組函數中，是同一個函數的是（ ）
A.
， 
B.f（x）=2log2x， 
C.f（x）=ln（x﹣1）﹣ln（x+1）， 
D.f（x）=lg（1﹣x）+lg（1+x），g（x）=lg（1﹣x2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=loga（x+1），（a＞0，a≠1）的圖象經過點（﹣ 
，﹣2），圖象上有三個點A，B，C，它們的橫坐標依次為t﹣1，t，t+1，（t≥1），記三角形ABC的面積為S（t），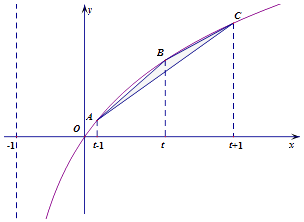 
（1）求f（x）的表達式；
（2）求S（1）；
（3）是否存在正整數m，使得對于一切不小于1的t，都有S（t）＜m，若存在求的最小值，若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知P（﹣2，3）是函數y= 
圖象上的點，Q是雙曲線在第四象限這一分支上的動點，過點Q作直線，使其與雙曲線y= 只有一個公共點，且與x軸、y軸分別交于點C、D，另一條直線y= 
x+6與x軸、y軸分別交于點A、B．則
（1）O為坐標原點，三角形OCD的面積為 ．
（2）四邊形ABCD面積的最小值為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
