
【題目】第三屆移動互聯創新大賽,于2017年3月~10月期間舉行,為了選出優秀選手,某高校先在計算機科學系選出一種子選手![]() ,再從全校征集出3位志愿者分別與
,再從全校征集出3位志愿者分別與![]() 進行一場技術對抗賽,根據以往經驗,
進行一場技術對抗賽,根據以往經驗, ![]() 與這三位志愿者進行比賽一場獲勝的概率分別為
與這三位志愿者進行比賽一場獲勝的概率分別為![]() ,且各場輸贏互不影響.
,且各場輸贏互不影響.
(1)求甲恰好獲勝兩場的概率;
(2)求甲獲勝場數的分布列與數學期望.
 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,以極點為平面直角坐標系的原點,極軸為
,以極點為平面直角坐標系的原點,極軸為![]() 的正半軸,建立平面直角坐標系
的正半軸,建立平面直角坐標系![]() .
.
(1)若曲線![]() 為參數)與曲線
為參數)與曲線![]() 相交于兩點
相交于兩點![]() ,求
,求![]() ;
;
(2)若![]() 是曲線
是曲線![]() 上的動點,且點
上的動點,且點![]() 的直角坐標為
的直角坐標為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地隨著經濟的發展,居民收入逐年增長.該地一建設銀行統計連續五年的儲蓄存款(年底余額)得到下表:
年份 |
|
|
|
|
|
儲蓄存款 (千億元) |
|
|
|
|
|
為便于計算,工作人員將上表的數據進行了處理(令![]() ,
, ![]() ),得到下表:
),得到下表:
時間 |
|
|
|
|
|
儲蓄存款 |
|
|
|
|
|
(Ⅰ)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(Ⅱ)通過(Ⅰ)中的方程,求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅲ)用所求回歸方程預測到![]() 年年底,該地儲蓄存款額可達多少?
年年底,該地儲蓄存款額可達多少?
附:線性回歸方程![]() ,其中
,其中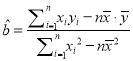 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() 六支足球隊參加單循環比賽(即任意兩支球隊只踢一場比賽),第一周的比賽中
六支足球隊參加單循環比賽(即任意兩支球隊只踢一場比賽),第一周的比賽中![]() ,各踢了
,各踢了![]() 場,
場, ![]() 各踢了
各踢了![]() 場,
場, ![]() 踢了
踢了![]() 場,且
場,且![]() 隊與
隊與![]() 隊未踢過,
隊未踢過, ![]() 隊與
隊與![]() 隊也未踢過,則在第一周的比賽中,
隊也未踢過,則在第一周的比賽中, ![]() 隊踢的比賽的場數是( )
隊踢的比賽的場數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com