【題目】已知函數f（x）=x2cos 
，數列{an}中，an=f（n）+f（n+1）（n∈N*），則數列{an}的前100項之和S100= ．
【答案】10200
【解析】解：∵f（x）=x2cos 
， ∴an=f（n）+f（n+1）= 
+ 
，
a4n﹣3= 
+（4n﹣2）2 
=﹣（4n﹣2）2 ，
同理可得：a4n﹣2=﹣（4n﹣2）2 ， a4n﹣1=（4n）2 ， a4n=（4n）2 ．
∴a4n﹣3+a4n﹣2+a4n﹣1+a4n=﹣2（4n﹣2）2+2（4n）2=8（4n﹣1）．
∴數列{an}的前100項之和S100=8×（3+7+…+99）=10200．
故答案為：10200．
f（x）=x2cos ，可得an=f（n）+f（n+1）= + ，分別求出a4n﹣3 ， a4n﹣2 ， a4n﹣1 ， a4n ， 再利用“分組求和”方法即可得出．
科目：高中數學 來源： 題型：
【題目】如圖，在正方體
中，過對角線
的一個平面交
于點
，交
于
.
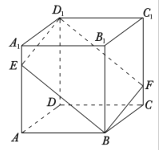
①四邊形
一定是平行四邊形；
②四邊形有可能是正方形；
③四邊形在底面
內的投影一定是正方形；
④四邊形有可能垂直于平面
．
以上結論正確的為_______________．（寫出所有正確結論的編號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓 
： 
，右頂點為 
，離心率為 
，直線 
： 
與橢圓 相交于不同的兩點 
， 
，過 
的中點 
作垂直于 的直線 
，設 與橢圓 相交于不同的兩點 ， 
，且 
的中點為 
．
（Ⅰ）求橢圓 的方程；
（Ⅱ）設原點 
到直線 的距離為 
，求 
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線 
﹣ 
=1（a＞0，b＞0）的實軸端點分別為A1 ， A2 ， 記雙曲線的其中的一個焦點為F，一個虛軸端點為B，若在線段BF上（不含端點）有且僅有兩個不同的點Pi（i=1，2），使得∠A1PiA2= 
，則雙曲線的離心率e的取值范圍是（ ）
A.（ 
， 
）
B.（ ， 
）
C.（1， ）
D.（ ，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下關于命題的說法正確的有（填寫所有正確命題的序號）．
①“若 
，則函數 
（ 
，且 
）在其定義域內是減函數”是真命題；
②命題“若 
，則 
”的否命題是“若 
，則 
”；
③命題“若 
， 
都是偶數，則 
也是偶數”的逆命題為真命題；
④命題“若 
，則 
”與命題“若 
，則 
”等價．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線的對稱軸為坐標軸，頂點是坐標原點，準線方程為 
，直線 
與拋物線相交于不同的 
， 
兩點．
（1）求拋物線的標準方程；
（2）如果直線 過拋物線的焦點，求 
的值；
（3）如果 
，直線 是否過一定點，若過一定點，求出該定點；若不過一定點，試說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，
是東西方向的公路北側的邊緣線，某公司準備在上的一點
的正北方向的
處建一倉庫，并在公路同側建造一個正方形無頂中轉站
（其中邊
在上），現從倉庫向和中轉站分別修兩條道路
，
，已知
，且
，設
，
．
（1）求
關于
的函數解析式；
（2）如果中轉站四周圍墻（即正方形周長）造價為
萬元
，兩條道路造價為
萬元，問：取何值時，該公司建中轉圍墻和兩條道路總造價
最低？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為了解游客人數的變化規律，提高旅游服務質量，收集并整理了2014年1月至2016年12月期間月接待游客量（單位：萬人）的數據，繪制了下面的折線圖.
根據該折線圖，下列結論錯誤的是（ ）
A.月接待游客逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相對于7月至12月，波動性更小，變化比較平穩
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
