【題目】已知橢圓
的左、右焦點分別是
，
，
，
是其左右頂點，點
是橢圓
上任一點，且
的周長為6，若
面積的最大值為
.
（1）求橢圓的方程；
（2）若過點
且斜率不為0的直線交橢圓于
，
兩個不同點，證明：直線
與
的交點在一條定直線上.
教材全解字詞句篇系列答案科目：高中數學 來源： 題型：
【題目】隨著移動互聯網的發展，與餐飲美食相關的手機
軟件層出不窮.為調查某款訂餐軟件的商家的服務情況，統計了10次訂餐“送達時間”，得到莖葉圖如下：（時間：分鐘）
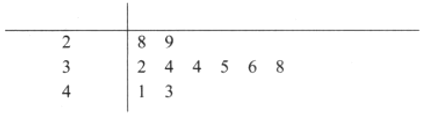
（1）請計算“送達時間”的平均數與方差：
（2）根據莖葉圖填寫下表：
送達時間 | 35分組以內（包括35分鐘） | 超過35分鐘 |
頻數 | A | B |
頻率 | C | D |
在答題卡上寫出
，
，
，
的值；
（3）在（2）的情況下，以頻率代替概率.現有3個客戶應用此軟件訂餐，求出在35分鐘以內（包括35分鐘）收到餐品的人數
的分布列，并求出數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某精準扶貧幫扶單位，為幫助定點扶貧村真正脫貧，堅持扶貧同扶智相結合，幫助精準扶貧戶利用互聯網電商渠道銷售當地特產蘋果.蘋果單果直徑不同單價不同，為了更好的銷售，現從該精準扶貧戶種植的蘋果樹上隨機摘下了50個蘋果測量其直徑，經統計，其單果直徑分布在區間[50，95]內（單位：
），統計的莖葉圖如圖所示：
（Ⅰ）按分層抽樣的方法從單果直徑落在[80，85），[85，90）的蘋果中隨機抽取6個，再從這6個蘋果中隨機抽取2個，求這兩個蘋果單果直徑均在[85，90）內的概率；
（Ⅱ）以此莖葉圖中單果直徑出現的頻率代表概率.已知該精準扶貧戶有20000個約5000千克蘋果待出售，某電商提出兩種收購方案：
方案
：所有蘋果均以5.5元/千克收購；
方案
：按蘋果單果直徑大小分3類裝箱收購，每箱裝25個蘋果，定價收購方式為：單果直徑 在[50，65）內按35元/箱收購，在[65，90）內按50元/箱收購，在[90，95]內按35元/箱收購.包裝箱與分揀裝箱工費為5元/箱.請你通過計算為該精準扶貧戶推薦收益最好的方案.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中的真命題是（ ）
A. 若
，則向量
與
的夾角為鈍角
B. 若
，則
C. 若命題“
是真命題”，則命題“
是真命題”
D. 命題“
，
”的否定是“
，
”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
的圓心坐標為
，且該圓經過點
.
（1）求圓的標準方程；
（2）若點
也在圓上，且弦
長為8，求直線的方程；
（3）直線
交圓于
，
兩點，若直線
，
的斜率之積為2，求證：直線過一個定點，并求出該定點坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在長方體ABCD-A1B1C1D1中（如圖），AD=AA1=1，AB=2，點E是棱AB的中點．
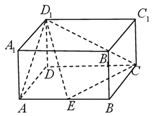
（1）求異面直線AD1與EC所成角的大小；
（2）《九章算術》中，將四個面都是直角三角形的四面體稱為鱉臑，試問四面體D1CDE是否為鱉臑？并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設O為坐標原點，動點M在橢圓C
上，過M作x軸的垂線，垂足為N，點P滿足
.
（1）求點P的軌跡方程；
（2）設點
在直線
上，且
.證明：過點P且垂直于OQ的直線
過C的左焦點F.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
