
(2005
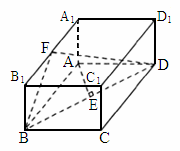
山東,20)如下圖,已知長方體 ,AB=2,
,AB=2, ,直線BD與平面
,直線BD與平面 所成的角為30°,AE垂直BD于E,F為
所成的角為30°,AE垂直BD于E,F為 的中點.
的中點.
(1)
求異面直線AE與BF所成的角;(2)
求平面BDF與平面 所成二面角(銳角)的大小;
所成二面角(銳角)的大小;
(3)
求點A到平面BDF的距離.|
解析:解法一:在長方體  中,以AB所在直線為x軸,AD所在直線為y軸, 中,以AB所在直線為x軸,AD所在直線為y軸,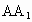 所在直線為z軸建立空間直角坐標系如下圖. 所在直線為z軸建立空間直角坐標系如下圖.
由已知 AB=2, ,可得A(0,0,0),B(2,0,0),F(1,0,1). ,可得A(0,0,0),B(2,0,0),F(1,0,1).
又 AD⊥平面 ,從而BD與平面 ,從而BD與平面 所成的角即為∠DBA=30°,又AB=2,AE⊥BD,AE=1, 所成的角即為∠DBA=30°,又AB=2,AE⊥BD,AE=1, , ,
從而易得  ,D ,D . .
(1) 因為 , ,
所以  . .
即異面直線 AE、BF所成的角為 . .
(2) 易知平面 的一個法向量m=(0,1,0). 的一個法向量m=(0,1,0).
設 n=(x,y,z)是平面BDF的一個法向量,
取 n=(1, ,1),∴ ,1),∴ , ,
即平面 BDF與平面 所成二面角(銳角)大小為 所成二面角(銳角)大小為 . .
(3) 點A到平面BDF的距離,即 在平面BDF的法向量n上的投影的絕對值. 在平面BDF的法向量n上的投影的絕對值.
所以距離 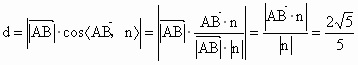 . .
所以點 A到平面BDF的距離為 . .
解法二:如下圖.
(1) 連結 ,過F作 ,過F作 的垂線,垂足為K, 的垂線,垂足為K,
∵  與兩底面ABCD, 與兩底面ABCD, 都垂直, 都垂直,
∴∠ BFK為異面直線BF與AE所成的角.連結BK,由FK⊥面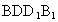 得FK⊥BK,從而△BKF為Rt△. 得FK⊥BK,從而△BKF為Rt△.
在 Rt△ 和Rt△ 和Rt△ 中,由 中,由 得 得
又  ,故 ,故 . .
∴異面直線 BF與AE所成的角為 . .
(2) 如下圖,由于DA⊥面 ,由A作BF的垂線AG,垂足為G.連結BG,由三垂線定理知BG⊥DG. ,由A作BF的垂線AG,垂足為G.連結BG,由三垂線定理知BG⊥DG.
∴∠ AGD即為平面BDF與平面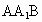 所成二面角的平面角. 所成二面角的平面角.
且∠ DAG=90°.在平面 中,延長BF與 中,延長BF與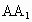 交于點S, 交于點S,
∵ F為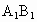 的中點, 的中點, , ,
∴ 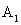 、F分別為SA、SB的中點,即 、F分別為SA、SB的中點,即 . .
∴ Rt△BAS為等腰三角形,垂足G點為斜邊SB的中點F,即F、G重合,易得  .在Rt△BAS中, .在Rt△BAS中, , ,
∴  , , . .
平面 BDF與平面 所成二面角(銳角)為 所成二面角(銳角)為 . .
(3) 如下圖,由(2)知平面AFD是平面BDF與平面 所成二面角的平面角所在的平面, 所成二面角的平面角所在的平面,
∴面 AFD⊥面BDF.在 Rt△ADF中,由A作AH⊥DF于H,則AH即為點A到平面BDF的距離.由  , ,
得 
所以點 A到平面BDF的距離為 . . |
|
剖析:本題考查線線角、線面角以及點面距離的求法,可用傳統綜合法或向量法求解. |


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com