
【題目】已知函數![]()
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)如果函數![]() 在公共定義域D上,滿足
在公共定義域D上,滿足![]() ,那么就稱
,那么就稱![]() 為
為![]() 的“伴隨函數”.已知函數
的“伴隨函數”.已知函數![]() ,
,![]() .若在區間
.若在區間![]() 上,函數
上,函數![]() 是
是![]() 的“伴隨函數”,求實數
的“伴隨函數”,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,正實數
,正實數![]() 滿足
滿足![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析
;(3)證明見解析
【解析】
(1)求出導函數![]() ,由導數研究函數的單調性得出最大值;
,由導數研究函數的單調性得出最大值;
(2)問題等價于![]() 對
對![]() 恒成立,
恒成立,
且![]() 對
對![]() 恒成立,利用導數研究不等式恒成立可得參數取值范圍;
恒成立,利用導數研究不等式恒成立可得參數取值范圍;
(3)把![]() ,變形為
,變形為![]() (令
(令![]() ),求出
),求出![]() 的最小值后解相應不等式(關于
的最小值后解相應不等式(關于![]() 的不等式),可得結論.
的不等式),可得結論.
解:(1)當![]() 時,
時,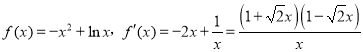 ,
,
當![]() 時,令
時,令![]() ,解得
,解得![]() .
.
列表如下:
|
|
|
|
|
| 0 |
|
| ↑ | 極大值 | ↓ |
所以,當![]() 時
時![]() 取得極大值,也即是最大值.
取得極大值,也即是最大值.
所以![]() 的最大值是
的最大值是![]()
(2)在區間![]() 上,函數
上,函數![]() 是
是![]() 的“伴隨函數”,則
的“伴隨函數”,則![]() ,令
,令![]() 對
對![]() 恒成立,
恒成立,
且![]() 對
對![]() 恒成立,
恒成立,
![]() (*)
(*)
①若![]() ,令
,令![]() ,得極值點
,得極值點![]() ,當
,當![]() ,即
,即![]() 時,在
時,在![]() 上有
上有![]() ,此時
,此時![]() 在區間
在區間![]() 上是增函數,并且在該區間上有
上是增函數,并且在該區間上有![]() ,不合題意;當
,不合題意;當![]() ,即
,即![]() 時,在
時,在![]() 上有
上有![]() ,此時
,此時![]() 在區間
在區間![]() 上是增函數,并且在該區間上有
上是增函數,并且在該區間上有![]() ,也不合題意;
,也不合題意;
②若![]() ,則有
,則有![]() ,此時在區間
,此時在區間![]() 上恒有
上恒有![]() ,
,
從而![]() 在區間
在區間![]() 上是減函數;要使
上是減函數;要使![]() 在此區間上恒成立,只需滿足
在此區間上恒成立,只需滿足![]() ,所以
,所以![]() .
.
又因為![]() 在
在![]() 上是減函數.
上是減函數.![]() ,所以
,所以![]() .
.
綜合可知![]() 的取值范圍是
的取值范圍是![]() .
.
(3)當![]() 時,
時,![]() .因為
.因為![]() ,
,
所以![]() .
.
令![]() ,則
,則![]() ,
,
令![]() 則
則![]() 令
令![]() 解得
解得![]() 當
當![]() 時,
時,![]()
![]() 在
在![]() 上單調遞增,當
上單調遞增,當![]() 時,
時,![]()
![]() 在
在![]() 上單調遞減,所以當
上單調遞減,所以當![]() 時
時![]() 取得極大值即最大值
取得極大值即最大值![]() ,所以
,所以![]() ,
,
解得![]()


科目:高中數學 來源: 題型:
【題目】某校高三年級共有學生![]() 名,為了解學生某次月考的情況,抽取了部分學生的成績(得分均為整數,滿分為
名,為了解學生某次月考的情況,抽取了部分學生的成績(得分均為整數,滿分為![]() 分)進行統計,繪制出如下尚未完成的頻率分布表:
分)進行統計,繪制出如下尚未完成的頻率分布表:
分組 | 頻數 | 頻率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)補充完整題中的頻率分布表;
(2)若成績在![]() 為優秀,估計該校高三年級學生在這次月考中,成績優秀的學生約為多少人.
為優秀,估計該校高三年級學生在這次月考中,成績優秀的學生約為多少人.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某村電費收取有以下兩種方案供農戶選擇:
方案一:每戶每月收取管理費2元,月用電量不超過30度時,每度0.5元;超過30度時,超過部分按每度0.6元收取:
方案二:不收取管理費,每度0.58元.
(1)求方案一的收費L(x)(元)與用電量x(度)間的函數關系.若老王家九月份按方案一繳費35元,問老王家該月用電多少度?
(2)老王家該月用電量在什么范圍內,選擇方案一比選擇方案二好?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學回答“用數學歸納法的證明![]() (n∈N*)”的過程如下:
(n∈N*)”的過程如下:
證明:①當n=1時,顯然命題是正確的.②假設當n=k(k≥1,k∈N*)時,有![]() ,那么當n=k+1時,
,那么當n=k+1時,![]() ,所以當n=k+1時命題是正確的,由①②可知對于n∈N*,命題都是正確的,以上證法是錯誤的,錯誤在于( )
,所以當n=k+1時命題是正確的,由①②可知對于n∈N*,命題都是正確的,以上證法是錯誤的,錯誤在于( )
A.從k到k+1的推理過程沒有使用歸納假設
B.假設的寫法不正確
C.從k到k+1的推理不嚴密
D.當n=1時,驗證過程不具體
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com