
設函數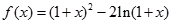 。
。
(Ⅰ)若在定義域內存在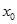 ,使不等式
,使不等式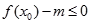 能成立,求實數
能成立,求實數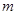 的最小值;
的最小值;
(Ⅱ)若函數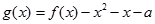 在區間
在區間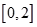 上恰有兩個不同的零點,求實數
上恰有兩個不同的零點,求實數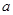 的取值范圍。
的取值范圍。
(1)1;(2)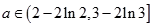
【解析】
試題分析:(1)不等式轉化為: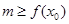 能成立,求m最小值。可以轉化成求函數
能成立,求m最小值。可以轉化成求函數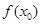 在定義域內的最小值。(2)函數
在定義域內的最小值。(2)函數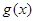 在
在 上有兩個不同零點,所以
上有兩個不同零點,所以 在
在 上有兩個不同的解,可以令
上有兩個不同的解,可以令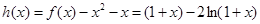 ,結合圖形研究函數
,結合圖形研究函數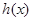 的性質即可。
的性質即可。
解答過程:(Ⅰ)要使得不等式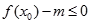 能成立,只需
能成立,只需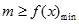 。 ………………1分
。 ………………1分
求導得: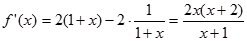 ,…………………………………2分
,…………………………………2分
∵函數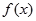 的定義域為
的定義域為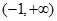 , ……………………………………3分
, ……………………………………3分
當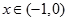 時,
時,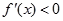 ,∴函數
,∴函數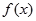 在區間
在區間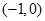 上是減函數;
上是減函數;
當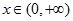 時,
時,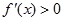 ,∴函數
,∴函數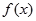 在區間(0,+∞)上是增函數。 …………5分
在區間(0,+∞)上是增函數。 …………5分
∴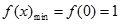 , ∴
, ∴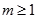 。故實數
。故實數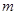 的最小值為1。……………………6分(Ⅱ)由
的最小值為1。……………………6分(Ⅱ)由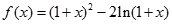 得:
得:
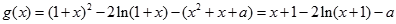 …………………7分
…………………7分
由題設可得:方程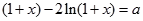 在區間
在區間 上恰有兩個相異實根。
上恰有兩個相異實根。
設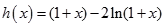 。∵
。∵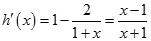 ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
|
減函數 |
|
增函數 |
|
∵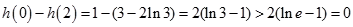 ,∴
,∴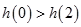 。
。
從而有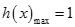 ,
,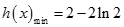
畫出函數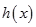 在區間
在區間 上的草圖(見圖),
上的草圖(見圖),

易知要使方程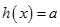 在區間
在區間 上恰有兩個相異實根,
上恰有兩個相異實根,
只需: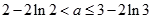 ,即:
,即: 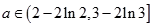 。 ……………12分
。 ……………12分
考點:本題考查了含參函數中參數的轉化問題,將存在性問題轉化為函數的最值和函數性質的研究,還需要借助圖象工具,數形結合,為一道水平較高的題目。
點評:本題需要靈活轉化,還要有一定邏輯分析能力和一定的計算能力,在難度上屬于中等偏上,第一問計算簡單,第二步計算在能力要求上有所增加。


科目:高中數學 來源: 題型:
| p |
| x |
| 2e |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| x |
| e |
| x |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省高三第一次階段考試理科數學試卷(解析版) 題型:解答題
(本小題滿分14分)設函數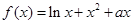 。
。
(1)若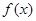 在
在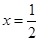 處取得極值,求
處取得極值,求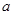 的值;
的值;
(2)若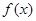 在定義域內為增函數,求
在定義域內為增函數,求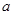 的取值范圍;
的取值范圍;
(3)設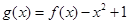 ,當
,當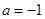 時,
時,
求證:① 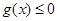 在其定義域內恒成立;
在其定義域內恒成立;
求證:② 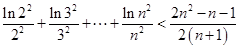 。
。
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| x |
| e |
| x |
查看答案和解析>>
科目:高中數學 來源:桂林模擬 題型:解答題
| p |
| x |
| 2e |
| x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com