Question

【題目】下列命題中正確命題的個數是（ ）

（1）若函數的定義域關于原點對稱，則為偶函數的充要條件為對任意的，都成立；

（2）若函數的定義域關于原點對稱，則“”是“為奇函數”的必要條件；

（3）函數對任意的實數都有，則在實數集上是增函數；

（4）已知函數在其定義域內有兩個不同的極值點，則實數的取值范圍是.

A.1B.2C.3D.4

Answer 1

【答案】B

【解析】

根據偶函數定義知（1）正確；若定義域不包含，可知必要性不成立，（2）錯誤；通過反例知（3）錯誤；將問題轉化為與函數在上有兩個交點，利用數形結合的方式可知（4）正確.

對于（1），根據偶函數的定義可得：若函數為偶函數，則對應定義域內的任意，都有；反之也成立；故（1）正確；

對于（2），函數的定義域不包含時，由“為奇函數”不能推出“”，故（2）錯誤；

對于（3），對于函數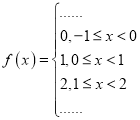，對于任意的實數都有，但不滿足在實數集上是增函數，故（3）錯誤；

對于（4），函數的定義域為，且，

令得：，即，構造函數，

則直線與函數在上有兩個交點.

，令，得，列表如下：

		0
		極大值

函數的單調遞增區間為，單調遞減區間為，極大值為，又時，，

可得圖象如下圖所示：

當時，直線與函數在上有兩個交點，

實數的取值范圍是，故（4）正確.

故選：.