Question

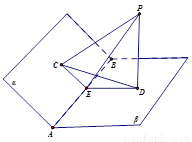
如圖，正方體ABCD—A₁B₁C₁D₁棱長為8，E、F分別為AD₁，CD₁中點，G、H分別為棱DA，DC上動點，且EH⊥FG．

（1）求GH長的取值范圍；

（2）當GH取得最小值時，求證：EH與FG共面；并求出此時EH與FG的交點P到直線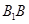的距離.

 

Answer 1

【答案】

（1）[2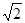，4] (2)

【解析】

試題分析：解：（1）以D為原點，DA，DC，DD₁分別為x軸，y軸，z軸建立空間直角坐標系．

設(shè)DG=a，DH=b，則E（4，0，4），F(xiàn)（0，4，4），G（a，0，0），H（0，b，0）．

∴=（－4，b，－4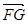），=（a，－4，－4）．

∵EH⊥FG．

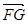∴·=－4a－4b+16=0，則a+b=4，即b=4－a．

又G₁H在棱DA，DC上，則0≤a≤8，0≤b≤8，從而0≤a≤4．

∴GH==．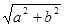

∴GH取值范圍是[2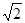，4] ．       ……6分

（2）當GH=2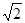時，a=2，b=2．

∴=（－2，2，0），=（－4，4，0），即=2．

∴EF∥GH，即EH與FG共面．

所以EF=2GH，EF∥GH，則．

設(shè)P（x₁，y₁，z₁），則=（x₁－4，y，z₁－4）．

∴x₁=，y₁=，z₁=，即P（，，）．

則P（，，）在底面上ABCD上的射影為M（，，0）.又B（8，8，0），

所以為點P到直線的距離.     ……12分

考點：空間中兩點的距離，點到直線的距離

點評：關(guān)鍵是通過建立空間直角坐標系，然后表示點的坐標以及點在平面的射影得到距離，屬于基礎(chǔ)題。