
已知橢圓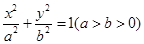 的右準(zhǔn)線
的右準(zhǔn)線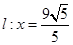 ,離心率
,離心率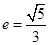 ,
, ,
, 是橢圓上的兩動點,動點
是橢圓上的兩動點,動點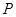 滿足
滿足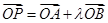 ,(其中
,(其中 為常數(shù)).
為常數(shù)).
(1)求橢圓標(biāo)準(zhǔn)方程;
(2)當(dāng)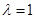 且直線
且直線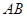 與
與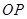 斜率均存在時,求
斜率均存在時,求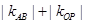 的最小值;
的最小值;
(3)若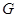 是線段
是線段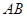 的中點,且
的中點,且 ,問是否存在常數(shù)
,問是否存在常數(shù) 和平面內(nèi)兩定點
和平面內(nèi)兩定點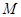 ,
,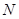 ,使得動點
,使得動點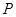 滿足
滿足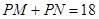 ,若存在,求出
,若存在,求出 的值和定點
的值和定點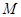 ,
,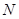 ;若不存在,請說明理由.
;若不存在,請說明理由.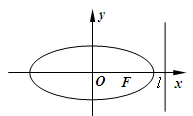
(1)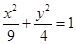 ;(2)
;(2)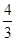 ;(3)
;(3) ,
,
解析試題分析:(1)根據(jù)題意由已知可得: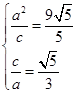 ,進(jìn)而求出基本量,得到橢圓方程;
,進(jìn)而求出基本量,得到橢圓方程; 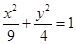 ;(2)由題中
;(2)由題中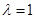 ,可得
,可得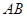 中點與原點的斜率即為
中點與原點的斜率即為 ,即可化簡得:
,即可化簡得: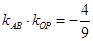 ,結(jié)合基本不等式求最值,即由
,結(jié)合基本不等式求最值,即由 得
得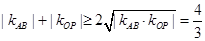 ;(3)由(2)中已求出
;(3)由(2)中已求出 ,即
,即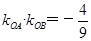 ,可化簡得:
,可化簡得: ,再結(jié)合條件
,再結(jié)合條件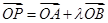 ,代入化簡可得:
,代入化簡可得: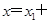



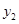 ,最后由點在橢圓上可得:
,最后由點在橢圓上可得: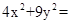
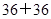
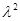


 ,即
,即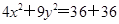
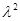 ,化簡即P點是橢圓
,化簡即P點是橢圓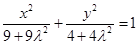 上的點,利用橢圓知識求出左、右焦點為
上的點,利用橢圓知識求出左、右焦點為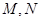 .
.
(I)由題設(shè)可知: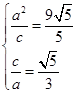 ∴
∴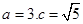 .又
.又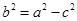 ,∴
,∴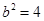 .
. 橢圓標(biāo)準(zhǔn)方程為
橢圓標(biāo)準(zhǔn)方程為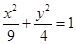 . 5分
. 5分
(2)設(shè)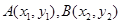 則由
則由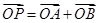 得
得 .
.
∴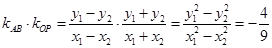 .
.
由 得
得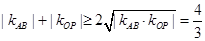 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)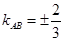 時取等號 10分
時取等號 10分
(3)
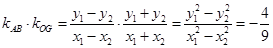 .
.
∴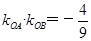 .∴
.∴ . 11分
. 11分
設(shè) ,則由
,則由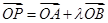 得
得

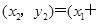

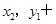

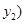 ,
,
即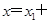


 y2. 因為點A、B在橢圓
y2. 因為點A、B在橢圓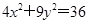 上,
上,
所以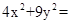
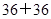
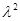


 .
.
所以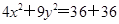
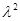 . 即
. 即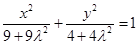 ,所以P點是橢圓
,所以P點是橢圓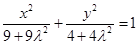 上的點,
上的點,
設(shè)該橢圓的左、右焦點為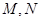 ,,則由橢圓的定義
,,則由橢圓的定義


科目:高中數(shù)學(xué) 來源: 題型:解答題
某小區(qū)想利用一矩形空地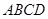 建市民健身廣場,設(shè)計時決定保留空地邊上的一水塘(如圖中陰影部分),水塘可近似看作一個等腰直角三角形,其中
建市民健身廣場,設(shè)計時決定保留空地邊上的一水塘(如圖中陰影部分),水塘可近似看作一個等腰直角三角形,其中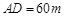 ,
,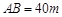 ,且
,且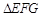 中,
中, ,經(jīng)測量得到
,經(jīng)測量得到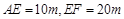 .為保證安全同時考慮美觀,健身廣場周圍準(zhǔn)備加設(shè)一個保護(hù)欄.設(shè)計時經(jīng)過點
.為保證安全同時考慮美觀,健身廣場周圍準(zhǔn)備加設(shè)一個保護(hù)欄.設(shè)計時經(jīng)過點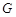 作一直線交
作一直線交 于
于 ,從而得到五邊形
,從而得到五邊形 的市民健身廣場,設(shè)
的市民健身廣場,設(shè)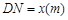 .
.
(1)將五邊形 的面積
的面積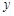 表示為
表示為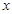 的函數(shù);
的函數(shù);
(2)當(dāng) 為何值時,市民健身廣場的面積最大?并求出最大面積.
為何值時,市民健身廣場的面積最大?并求出最大面積.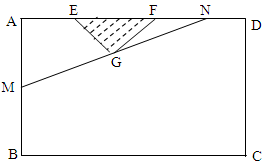
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如下圖所示,橢圓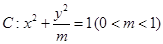 的左頂點為
的左頂點為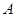 ,
,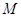 是橢圓
是橢圓 上異于點
上異于點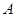 的任意一點,點
的任意一點,點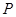 與點
與點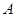 關(guān)于點
關(guān)于點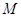 對稱.
對稱.
(1)若點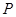 的坐標(biāo)為
的坐標(biāo)為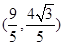 ,求
,求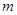 的值;
的值;
(2)若橢圓 上存在點
上存在點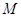 ,使得
,使得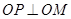 ,求
,求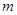 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
要制作一個如圖的框架(單位:m),要求所圍成的總面積為19.5(m2),其中ABCD是一個矩形,EFCD是一個等腰梯形,梯形高h(yuǎn)=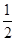 AB,tan∠FED=
AB,tan∠FED=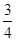 ,設(shè)AB=xm,BC=y(tǒng)m.
,設(shè)AB=xm,BC=y(tǒng)m.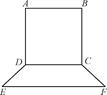
(1)求y關(guān)于x的表達(dá)式;
(2)如何設(shè)計x、y的長度,才能使所用材料最少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知橢圓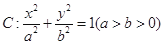 的離心率為
的離心率為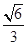 ,短軸一個端到右焦點的距離為
,短軸一個端到右焦點的距離為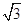 .
.
(Ⅰ)求橢圓C的方程:
(Ⅱ)設(shè)直線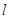 與橢圓C交于A、B兩點,坐標(biāo)原點O到直線
與橢圓C交于A、B兩點,坐標(biāo)原點O到直線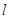 的距離為
的距離為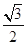 ,求△AOB面積的最大值.
,求△AOB面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(12分)利用基本不等式求最值:
(1)若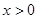 ,求函數(shù)
,求函數(shù)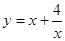 的最小值,并求此時x的值.
的最小值,并求此時x的值.
(2)設(shè)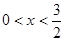 ,求函數(shù)
,求函數(shù)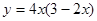 的最大值.
的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com