Question

【題目】已知函數.

（Ⅰ）若,求曲線在點處的切線方程;

（Ⅱ）若,求函數的單調區間;

（Ⅲ）若,求證: .

Answer 1

【答案】（Ⅰ）；（Ⅱ） ；（Ⅲ）證明見解析.

【解析】試題分析：（Ⅰ）求出求出的值可得切點坐標，求出的值，可得切線斜率，利用點斜式可得曲線在點處的切線方程；（Ⅱ）在定義域內，分別令求得的范圍，可得函數增區間， 求得的范圍，可得函數的減區間；（Ⅲ） ,等價于,等價于，設,只須證成立，利用導數研究函數的單調性，利用單調性求出的最小值，證明最小值大于零即可得結論.

試題解析：（Ⅰ）若,則,,

所以在點處的切線方程為.

（Ⅱ）

令,則.

令,得 (依題意)

由,得;由,得.

所以, 在區間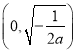上單調遞減,在區間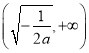上單調遞增,所以,

因為,所以.

所以,即.

所以函數的單調遞增區間為.

（Ⅲ）由,等價于,

等價于.

設,只須證成立.

因為

由,得有異號兩根.

令其正根為,則.

在上,在上

則的最小值為

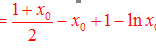
又

所以則

因此即所以.所以.

【方法點晴】本題主要考查利用導數求曲線切線方程以及利用導數研究函數的單調性、證明不等式，屬于難題.求曲線切線方程的一般步驟是：（1）求出在處的導數，即在點 出的切線斜率（當曲線在處的切線與軸平行時，在 處導數不存在，切線方程為）；（2）由點斜式求得切線方程.