
【題目】已知橢圓![]() 的離心率
的離心率![]() ,左頂點
,左頂點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,若以
兩點,若以![]() 為直徑的圓經過坐標原點,證明:
為直徑的圓經過坐標原點,證明:![]() 到直線
到直線![]() 的距離為定值.
的距離為定值.
【答案】(1)![]() .(2)見解析
.(2)見解析
【解析】
(1)結合離心率![]() ,計算出a,b,c之間的關系,利用點到直線距離,計算a,b值,即可。(2)分直線AB斜率存在與不存在討論,結合直線方程和橢圓方程,并利用
,計算出a,b,c之間的關系,利用點到直線距離,計算a,b值,即可。(2)分直線AB斜率存在與不存在討論,結合直線方程和橢圓方程,并利用![]() ,計算O到直線距離,即可.
,計算O到直線距離,即可.
(1)∵橢圓![]() 的離心率
的離心率![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∵橢圓![]() 的左頂點
的左頂點![]() 到直線
到直線![]() ,即到
,即到![]() 的距離
的距離![]() ,
,
∴![]() ,
,
把![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,![]() ,
,
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)設![]() ,
,
①當直線![]() 的斜率不存在時,由橢圓的性質可得:
的斜率不存在時,由橢圓的性質可得:![]() ,
,![]() ,
,
∵當直線![]() 的斜率不存在時,以
的斜率不存在時,以![]() 為直徑的圓經過坐標原點,
為直徑的圓經過坐標原點,
∴![]() ,即
,即![]() ,也就是
,也就是![]() ,
,
又∵點![]() 在橢圓
在橢圓![]() 上, ∴
上, ∴![]() ,
,
∵以![]() 為直徑的圓經過坐標原點,且
為直徑的圓經過坐標原點,且![]() 平行于
平行于![]() 軸,
軸,
∴![]() ,∴
,∴![]() ,解得:
,解得:![]()
此時點![]() 到直線
到直線![]() 的距離
的距離![]()
②當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
與橢圓方程聯立有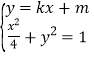 ,消去
,消去![]() ,得
,得![]()
∴![]() ,
,![]() ,
,
同理: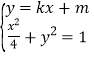 ,消去
,消去![]() ,得
,得![]() ,
,
即![]() ,∴
,∴![]()
∵![]() 為直徑的圓過坐標原點
為直徑的圓過坐標原點![]() ,所以
,所以![]() ,∴
,∴![]()
∴![]()
∴![]()
∴![]()
∴點![]() 到直線
到直線![]() 的距離
的距離![]()
綜上所述,點![]() 到直線
到直線![]() 的距離為定值
的距離為定值![]() .
.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】某網店經營的一種商品進行進價是每件10元,根據一周的銷售數據得出周銷售量![]() (件)與單價
(件)與單價![]() (元)之間的關系如下圖所示,該網店與這種商品有關的周開支均為25元.
(元)之間的關系如下圖所示,該網店與這種商品有關的周開支均為25元.

(1)根據周銷售量圖寫出![]() (件)與單價
(件)與單價![]() (元)之間的函數關系式;
(元)之間的函數關系式;
(2)寫出利潤![]() (元)與單價
(元)與單價![]() (元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.
(元)之間的函數關系式;當該商品的銷售價格為多少元時,周利潤最大?并求出最大周利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
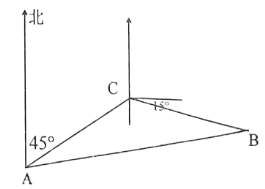
【題目】宿州泗縣石龍湖國家濕地公園是保存完好的典型濕地生態系統,具有得天獨厚的旅游資源.某日一游船在湖上游玩航行中突然遇險,發出呼救信號,駐湖救援隊在![]() 處獲悉后,立即測出該游船在北偏東
處獲悉后,立即測出該游船在北偏東![]() 方向上,距離
方向上,距離![]() 有
有![]() 千米的
千米的![]() 處,并測得游船正沿東偏南
處,并測得游船正沿東偏南![]() 的方向,以
的方向,以![]() 千米/時的速度向湖心小島
千米/時的速度向湖心小島![]() 靠攏,救援艦艇立即以
靠攏,救援艦艇立即以![]() 千米/時的速度前去營救,若想用最短的時間營救游船,求艦艇的航行方向和所需時間.
千米/時的速度前去營救,若想用最短的時間營救游船,求艦艇的航行方向和所需時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() .若滿射
.若滿射![]() ,滿足:對任意的
,滿足:對任意的![]() ,
,![]() ,則稱
,則稱![]() 為“和諧函數”.記
為“和諧函數”.記 ![]() ,
,![]() .設“和諧映射”
.設“和諧映射”![]() 為滿足條件:存在正整數
為滿足條件:存在正整數![]() ,使得(1)當
,使得(1)當![]() 時,若
時,若![]() ,
,![]() ,則
,則![]()
![]()
![]() ;(2)若
;(2)若![]() ,
,![]() ,則
,則![]() ,求
,求![]() 的最大可能值.
的最大可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一種排卡游戲規則如下:將寫有![]() 的九張卡片隨機地排成一行,第一張卡片:左起)上的標數為
的九張卡片隨機地排成一行,第一張卡片:左起)上的標數為![]() ,則將前
,則將前![]() 張卡片逆序排過來稱為一次操作,無法操作時(即第一張卡片上的標數“1”)游戲停止.若一個排列無法操作,且恰由唯一的另一個排列經過一次操作得到,則此排列稱為“二次終止排列”.在所有可能的排列中,求二次終止排列出現的概率.
張卡片逆序排過來稱為一次操作,無法操作時(即第一張卡片上的標數“1”)游戲停止.若一個排列無法操作,且恰由唯一的另一個排列經過一次操作得到,則此排列稱為“二次終止排列”.在所有可能的排列中,求二次終止排列出現的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有5個匣子,每個匣子有一把鑰匙,并且鑰匙不能通用.如果隨意在每一個匣內放入一把鑰匙,然后把匣子全都鎖上.現在允許砸開一個匣子,使得能相繼用鑰匙打開其余4個匣子,那么鑰匙的放法有______種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,其中
,其中![]() ,
,![]() 是函數
是函數![]() 定義城內任意不相等的兩個實數.
定義城內任意不相等的兩個實數.
(1)若![]() ,同時
,同時![]() ,求證:
,求證:![]() ;
;
(2)判斷![]() 是否在集合A中,并說明理由;
是否在集合A中,并說明理由;
(3)設函數![]() 的定義域為B,函數
的定義域為B,函數![]() 的值域為C.函數
的值域為C.函數![]() 滿足以下3個條件:
滿足以下3個條件:
①![]() ,②
,②![]() ,③
,③![]() .試確定一個滿足以上3個條件的函數
.試確定一個滿足以上3個條件的函數![]() 要對滿足的條件進行說明).
要對滿足的條件進行說明).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com