
【題目】![]() 統(tǒng)計(jì)學(xué)中將
統(tǒng)計(jì)學(xué)中將![]() 個數(shù)
個數(shù)![]() 的和記作
的和記作![]()
(1)設(shè)![]()
![]() ,求
,求![]() ;
;
(2)是否存在互不相等的非負(fù)整數(shù)![]() ,
,![]() ,使得
,使得![]() 成立,若存在,請寫出推理的過程;若不存在請證明;
成立,若存在,請寫出推理的過程;若不存在請證明;
(3)設(shè)![]()
![]() 是不同的正實(shí)數(shù),
是不同的正實(shí)數(shù),![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,判斷
,判斷![]() 是否為一個等比數(shù)列,請說明理由.
是否為一個等比數(shù)列,請說明理由.
【答案】(1)79;(2)不存在,證明詳見解析;(3)是等比數(shù)列,理由詳見解析.
【解析】
(1)代值計(jì)算結(jié)果.(2)距離2019最近的2的冪次為![]() ,而2019小于2048,所以
,而2019小于2048,所以![]() ,但是2048和2019的差不大,所以可以研究他們的差如何表示.(3)利用數(shù)學(xué)歸納法證明.
,但是2048和2019的差不大,所以可以研究他們的差如何表示.(3)利用數(shù)學(xué)歸納法證明.
(1)因?yàn)?/span>![]() ,所以
,所以![]()
所以![]()
(2)因?yàn)?/span>![]() ,
,![]()
又![]() ,所以
,所以![]() 中最大可能是10,
中最大可能是10,
因?yàn)?/span>![]() ,
,
![]()
所以![]()
又![]() ,
,
所以必有![]() ·
·
又因?yàn)?/span>![]() ,所以
,所以![]()
所以必然存在某幾項(xiàng)![]() ,其中
,其中![]() ,
,
只有![]() ,
,
所以存在這樣互不相等的非負(fù)整數(shù)![]() ,
,![]() ,
,
使得![]() 成立。
成立。
(3)數(shù)學(xué)歸納法證明:
當(dāng)![]() ,代入
,代入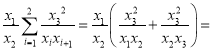
![]() ,
,
化簡得![]() 所以
所以![]() 成等比數(shù)列
成等比數(shù)列
假設(shè)當(dāng)![]() 時
時![]() 成等比數(shù)列,
成等比數(shù)列,![]() 是不同的正實(shí)數(shù)
是不同的正實(shí)數(shù)
記![]() ,設(shè)
,設(shè)![]()
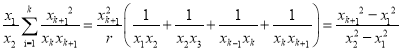
化簡整理得:
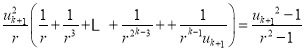
去分母同乘以![]() 得
得
![]()
整理![]()
![]()
因?yàn)?/span>![]()
得![]() ,從而
,從而![]() ,
,
所以![]() 時
時![]() 是等比數(shù)列
是等比數(shù)列


 口算能手系列答案
口算能手系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為踐行“綠水青山就是金山銀山”的發(fā)展理念和提高生態(tài)環(huán)境的保護(hù)意識,高二年級準(zhǔn)備成立一個環(huán)境保護(hù)興趣小組.該年級理科班有男生400人,女生200人;文科班有男生100人,女生300人.現(xiàn)按男、女用分層抽樣從理科生中抽取6人,按男、女分層抽樣從文科生中抽取4人,組成環(huán)境保護(hù)興趣小組,再從這10人的興趣小組中抽出4人參加學(xué)校的環(huán)保知識競賽.
(1)設(shè)事件![]() 為“選出的這4個人中要求有兩個男生兩個女生,而且這兩個男生必須文、理科生都有”,求事件
為“選出的這4個人中要求有兩個男生兩個女生,而且這兩個男生必須文、理科生都有”,求事件![]() 發(fā)生的概率;
發(fā)生的概率;
(2)用![]() 表示抽取的4人中文科女生的人數(shù),求
表示抽取的4人中文科女生的人數(shù),求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△![]() 的內(nèi)角
的內(nèi)角![]() 、
、![]() 、
、![]() 的對邊分別為
的對邊分別為![]() 、
、![]() 、
、![]() ,其中
,其中![]() ,且
,且![]() ,延長線段
,延長線段![]() 到點(diǎn)
到點(diǎn)![]() ,使得
,使得![]() ,
,![]() .
.
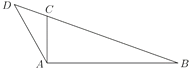
(1)求證:![]() 是直角;
是直角;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如果存在常數(shù)a,使得數(shù)列{an}滿足:若x是數(shù)列{an}中的一項(xiàng),則a-x也是數(shù)列{an}中的一項(xiàng),稱數(shù)列{an}為“兌換數(shù)列”,常數(shù)a是它的“兌換系數(shù)”.
(1)若數(shù)列:2,3,6,m(m>6)是“兌換系數(shù)”為a的“兌換數(shù)列”,求m和a的值;
(2)已知有窮等差數(shù)列{bn}的項(xiàng)數(shù)是n0(n0≥3),所有項(xiàng)之和是B,求證:數(shù)列{bn}是“兌換數(shù)列”,并用n0和B表示它的“兌換系數(shù)”;
(3)對于一個不少于3項(xiàng),且各項(xiàng)皆為正整數(shù)的遞增數(shù)列{cn},是否有可能它既是等比數(shù)列,又是“兌換數(shù)列”?給出你的結(jié)論,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)參加![]() 項(xiàng)目生產(chǎn)的工人為
項(xiàng)目生產(chǎn)的工人為![]() 人,平均每人每年創(chuàng)造利潤
人,平均每人每年創(chuàng)造利潤![]() 萬元.根據(jù)現(xiàn)實(shí)的需要,從
萬元.根據(jù)現(xiàn)實(shí)的需要,從![]() 項(xiàng)目中調(diào)出
項(xiàng)目中調(diào)出![]() 人參與
人參與![]() 項(xiàng)目的售后服務(wù)工作,每人每年可以創(chuàng)造利潤
項(xiàng)目的售后服務(wù)工作,每人每年可以創(chuàng)造利潤![]() 萬元(
萬元(![]() ),
),![]() 項(xiàng)目余下的工人每人每年創(chuàng)造利圖需要提高
項(xiàng)目余下的工人每人每年創(chuàng)造利圖需要提高![]()
(1)若要保證![]() 項(xiàng)目余下的工人創(chuàng)造的年總利潤不低于原來
項(xiàng)目余下的工人創(chuàng)造的年總利潤不低于原來![]() 名工人創(chuàng)造的年總利潤,則最多調(diào)出多少人參加
名工人創(chuàng)造的年總利潤,則最多調(diào)出多少人參加![]() 項(xiàng)目從事售后服務(wù)工作?
項(xiàng)目從事售后服務(wù)工作?
(2)在(1)的條件下,當(dāng)從![]() 項(xiàng)目調(diào)出的人數(shù)不能超過總?cè)藬?shù)的
項(xiàng)目調(diào)出的人數(shù)不能超過總?cè)藬?shù)的![]() 時,才能使得
時,才能使得![]() 項(xiàng)目中留崗工人創(chuàng)造的年總利潤始終不低于調(diào)出的工人所創(chuàng)造的年總利潤,求實(shí)數(shù)
項(xiàng)目中留崗工人創(chuàng)造的年總利潤始終不低于調(diào)出的工人所創(chuàng)造的年總利潤,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱錐P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一點(diǎn),且CD⊥平面PAB.

(1)求證:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某旅游勝地欲開發(fā)一座景觀山,從山的側(cè)面進(jìn)行勘測,迎面山坡線![]() 由同一平面的兩段拋物線組成,其中
由同一平面的兩段拋物線組成,其中![]() 所在的拋物線以
所在的拋物線以![]() 為頂點(diǎn)、開口向下,
為頂點(diǎn)、開口向下,![]() 所在的拋物線以
所在的拋物線以![]() 為頂點(diǎn)、開口向上,以過山腳(點(diǎn)
為頂點(diǎn)、開口向上,以過山腳(點(diǎn)![]() )的水平線為
)的水平線為![]() 軸,過山頂(點(diǎn)
軸,過山頂(點(diǎn)![]() )的鉛垂線為
)的鉛垂線為![]() 軸建立平面直角坐標(biāo)系如圖(單位:百米).已知
軸建立平面直角坐標(biāo)系如圖(單位:百米).已知![]() 所在拋物線的解析式
所在拋物線的解析式![]() ,
,![]() 所在拋物線的解析式為
所在拋物線的解析式為![]()
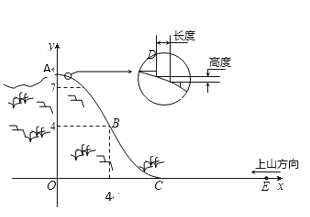
(1)求![]() 值,并寫出山坡線
值,并寫出山坡線![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)在山坡上的700米高度(點(diǎn)![]() )處恰好有一小塊平地,可以用來建造索道站,索道的起點(diǎn)選擇在山腳水平線上的點(diǎn)
)處恰好有一小塊平地,可以用來建造索道站,索道的起點(diǎn)選擇在山腳水平線上的點(diǎn)![]() 處,
處,![]() (米),假設(shè)索道
(米),假設(shè)索道![]() 可近似地看成一段以
可近似地看成一段以![]() 為頂點(diǎn)、開口向上的拋物線
為頂點(diǎn)、開口向上的拋物線![]() 當(dāng)索道在
當(dāng)索道在![]() 上方時,索道的懸空高度有最大值,試求索道的最大懸空高度;
上方時,索道的懸空高度有最大值,試求索道的最大懸空高度;
(3)為了便于旅游觀景,擬從山頂開始、沿迎面山坡往山下鋪設(shè)觀景臺階,臺階每級的高度為20厘米,長度因坡度的大小而定,但不得少于20厘米,每級臺階的兩端點(diǎn)在坡面上(見圖).試求出前三級臺階的長度(精確到厘米),并判斷這種臺階能否一直鋪到山腳,簡述理由?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圖1是某斜拉式大橋圖片,為了了解橋的一些結(jié)構(gòu)情況,學(xué)校數(shù)學(xué)興趣小組將大橋的結(jié)構(gòu)進(jìn)行了簡化,取其部分可抽象成圖2所示的模型,其中橋塔![]() 、
、![]() 與橋面
與橋面![]() 垂直,通過測量得知
垂直,通過測量得知![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 為
為![]() 中點(diǎn)時,
中點(diǎn)時,![]() .
.
(1)求![]() 的長;
的長;
(2)試問![]() 在線段
在線段![]() 的何處時,
的何處時,![]() 達(dá)到最大.
達(dá)到最大.

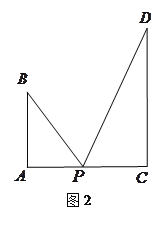
圖1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義:若函數(shù)![]() 對任意的
對任意的![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 為
為![]() 上的“淡泊”函數(shù).
上的“淡泊”函數(shù).
(1)判斷![]() 是否為
是否為![]() 上的“淡泊”函數(shù),說明理由;
上的“淡泊”函數(shù),說明理由;
(2)是否存在實(shí)數(shù)![]() ,使
,使![]() 為
為![]() 上的“淡泊”函數(shù),若存在,求出
上的“淡泊”函數(shù),若存在,求出![]() 的取值范圍;不存在,說明理由;
的取值范圍;不存在,說明理由;
(3)設(shè)![]() 是
是![]() 上的“淡泊”函數(shù)(其中
上的“淡泊”函數(shù)(其中![]() 不是常值函數(shù)),且
不是常值函數(shù)),且![]() ,若對任意的
,若對任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com