
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 為
為![]() 中點,
中點, ![]() 是棱
是棱![]() 上的點,
上的點, ![]() .
.
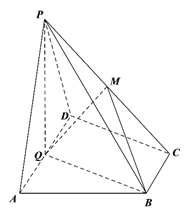
(Ⅰ)若點![]() 是棱
是棱![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)若二面角![]() 為
為![]() ,設
,設![]() ,試確定
,試確定![]() 的值.
的值.
【答案】(I)詳見解析;(II)詳見解析;(III)![]() .
.
【解析】試題分析:(Ⅰ)連接![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,證得
,證得![]() ,再利用線面平行的判定定理,證得
,再利用線面平行的判定定理,證得![]() 平面
平面![]() ;
;
(Ⅱ)因為![]() 為
為![]() 中點,得到
中點,得到![]() ,進而得到
,進而得到![]() 平面
平面![]() ,利用面面垂直的判定定理,即可證明平面
,利用面面垂直的判定定理,即可證明平面![]() 平面
平面![]() ;
;
(Ⅲ)以![]() 為原點,以
為原點,以![]() 的方向分別為
的方向分別為![]() 軸,
軸, ![]() 軸的正方向,建立如圖所示的空間直角坐標系,求得平面
軸的正方向,建立如圖所示的空間直角坐標系,求得平面![]() 的一個法向量
的一個法向量![]() 和平面
和平面![]() 中,
中, ![]() ,利用向量的夾角公式,即可求得
,利用向量的夾角公式,即可求得![]() 的值.
的值.
試題解析:
(Ⅰ)證明:連接![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,
,
因為![]() 且
且![]() ,即
,即![]() 且
且![]()
所以四邊形![]() 為平行四邊形,且
為平行四邊形,且![]() 為
為![]() 中點,
中點,
又因為![]() 是
是![]() 中點,
中點,
所以![]() ,
,
因為![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
(Ⅱ)因為![]() 為
為![]() 中點,
中點,
所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() .
.
因為![]() ,所以
,所以![]() ,即
,即![]() .
.
又因為平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅲ)因為![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
又因為平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
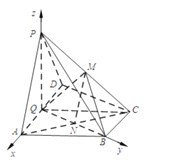
以![]() 為原點,以
為原點,以![]() 的方向分別為
的方向分別為![]() 軸,
軸, ![]() 軸的正方向,
軸的正方向,
建立如圖所示的空間直角坐標系![]() ,
,
則點![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 的一個法向量
的一個法向量![]() .
.
設![]() ,則
,則![]() ,
,![]() ,
,
因為![]()
所以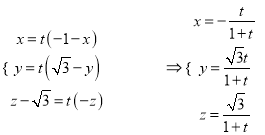
在平面![]() 中,
中, 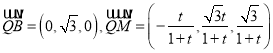 ,
,
因為二面角![]() 為
為![]() ,
,
所以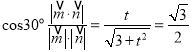 ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】若![]() 是各項均為正數的數列
是各項均為正數的數列![]() 的前
的前![]() 項和,且
項和,且![]() .
.
(1)求![]() 的值;
的值;
(2)設![]() ,且數列
,且數列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() 對任意正整數
對任意正整數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)設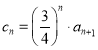 ,問:是否存在正整數
,問:是否存在正整數![]() ,使得
,使得![]() 對一切正整數
對一切正整數![]() 恒成立?若存在,請求出實數
恒成立?若存在,請求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某物流公司引進了一套無人智能配貨系統,購買系統的費用為80萬元,維持系統正常運行的費用包括保養費和維修費兩部分,每年的保養費用為1萬元.該系統的維修費為:第一年![]() 萬元,第二年
萬元,第二年![]() 萬元,第三年2萬元,…,依等差數列逐年遞增.
萬元,第三年2萬元,…,依等差數列逐年遞增.
(1)求該系統使用n年的總費用![]() (包括購買設備的費用);
(包括購買設備的費用);
(2)求該系統使用多少年報廢,使年平均費用最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,滿足
上,滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 過點
過點![]() ,且與橢圓只有一個公共點,直線
,且與橢圓只有一個公共點,直線![]() 與
與![]() 的傾斜角互補,且與橢圓交于異于點
的傾斜角互補,且與橢圓交于異于點![]() 的兩點
的兩點![]() ,
,![]() ,與直線
,與直線![]() 交于點
交于點![]() (
(![]() 介于
介于![]() ,
,![]() 兩點之間).
兩點之間).
(i)求證:![]() ;
;
(ii)是否存在直線![]() ,使得直線
,使得直線![]() 、
、![]() 、
、![]() 、
、![]() 的斜率按某種順序能構成等比數列?若能,求出
的斜率按某種順序能構成等比數列?若能,求出![]() 的方程;若不能,請說明理由.
的方程;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校在學校內招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者.將這
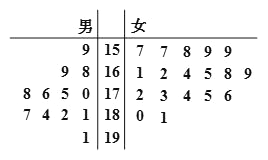
名女志愿者.將這![]() 名志愿者的身高編成如右莖葉圖(單位:
名志愿者的身高編成如右莖葉圖(單位: ![]() ),若身高在
),若身高在![]() 以上(包括
以上(包括![]() )定義為“高個子”,身高在
)定義為“高個子”,身高在![]() 以下(不包括
以下(不包括![]() )定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
)定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
(Ⅰ)如果用分層抽樣的方法從“高個子”和“非高個子”中抽取![]() 人,再從這
人,再從這![]() 人中選
人中選![]() 人,那么至少有一人是“高個子”的概率是多少?
人,那么至少有一人是“高個子”的概率是多少?
(Ⅱ)若從所有“高個子”中選![]() 名志愿者,用
名志愿者,用![]() 表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出
表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出![]() 的分布列,并求
的分布列,并求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M的方程為![]() ,直線l的方程為
,直線l的方程為![]() ,點P在直線l上,過P點作圓M的切線
,點P在直線l上,過P點作圓M的切線![]() ,
,![]() ,切點為A,B.
,切點為A,B.
(1)若![]() ,試求點P的坐標;
,試求點P的坐標;
(2)求證:經過A,P,M三點的圓必過定點,并求出所有定點的坐標;
(3)設線段![]() 的中點為N,求點N的軌跡方程.
的中點為N,求點N的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·全國Ⅲ卷)已知數列{an}的前n項和Sn=1+λan,其中λ≠0.
(1)證明{an}是等比數列,并求其通項公式;
(2)若S5=![]() ,求λ.
,求λ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且
,且![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(點
兩點(點![]() 均在第一象限),且直線
均在第一象限),且直線![]() 的斜率成等比數列,證明:直線
的斜率成等比數列,證明:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com