
���}Ŀ��ij��ÿ�괺��(ji��)ǰ��,���ڴ����ğ��������ȼ��,�՚���Ⱦ�^���(y��n)�أ�ԓ�Эh(hu��n)���о�����(du��)���괺��(ji��)ǰ��ÿ��Ŀ՚���Ⱦ��r�{(di��o)���о���l(f��)�F(xi��n),ÿ��՚���Ⱦ��ָ��(sh��)��f��t�����S�r(sh��)��t���r(sh��)��׃����Ҏ(gu��)�ɝM����_(d��)ʽ![]() ������a��՚������{(di��o)��(ji��)����(sh��),��a�ʣ�0��1����
������a��՚������{(di��o)��(ji��)����(sh��),��a�ʣ�0��1����
(1)��![]() ,��x��ȡֵ������
,��x��ȡֵ������
(2)��Ҏ(gu��)��ÿ����f��t�������ֵ���鮔(d��ng)��Ŀ՚���Ⱦָ��(sh��),Ҫʹԓ��ÿ��Ŀ՚���Ⱦָ��(sh��)�����^(gu��)5,ԇ���{(di��o)��(ji��)����(sh��)a��ȡֵ������
���𰸡�(1)[0��1]��(2)![]() .
.
��������
(1)�}����(j��)t��ȡֵ����������(f��)�Ϻ���(sh��)ͬ���Ć��{(di��o)�Կɵ�x��ȡֵ������
(2)�}����(j��)��(1)�}����ʾ��(g��u)��һ��(g��)����(sh��)h��x��=|x-a|+3a+2��Ȼ�^��(du��)ֵ����(sh��)�D(zhu��n)���ɷֶκ���(sh��)�����]���{(di��o)�Լ����ֵ��ȡֵ�����c5���^�����ɵõ��{(di��o)��(ji��)����(sh��)a��ȡֵ������
(1)���}��,0��t��24���t1��![]() t+1��10,
t+1��10,
��0=lg1��lg��![]() t+1����lg10=1��
t+1����lg10=1��
��x��ȡֵ�����飺[0��1]��
(2)��(1),֪�� ![]()
���O(sh��)![]()
�t![]() ��
��
����(j��)һ�κ���(sh��)�Ć��{(di��o)��,�����@h��x����[0��a���φ��{(di��o)�f�p,��[a��1]�φ��{(di��o)�f����
����![]() ��ʾ����(sh��)�����ֵ��
��ʾ����(sh��)�����ֵ��![]() ������ֵ.
������ֵ.
��![]() ��
��
��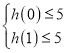 ,��
,��![]() ,
,
���0��a��![]() ��
��
��a��ȡֵ�����飺��0��![]() ]��
]��


 ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һԪ���η���x2-mx+m2+m-1=0�ЃɌ�(sh��)��x1��x2��
��1����m��ȡֵ������
��2����x1x2����ֵ��
��3�����![]() ����m��ȡֵ������
����m��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij������˾ُ(g��u)�I(m��i)��һ�K�L(zh��ng)AM��90�ף���AN��30�ľ��ε؉KAMPN��Ҏ(gu��)�����O(sh��)ռ����D�о���ABCD�Ă}(c��ng)��(k��)������ط����·��ͣ܇��(ch��ng)��Ҫ����c(di��n)C�ڵ؉K��(du��)�Ǿ�MN�ϣ�B��D�քe��߅AM��AN�ϣ����O(sh��)AB�L(zh��ng)�Ȟ�x�ף���Ҏ(gu��)�����O(sh��)�Ă}(c��ng)��(k��)�Ǹ߶��cAB���L(zh��ng)��ͬ���L(zh��ng)���w��������(w��n)AB�L(zh��ng)����ٕr(sh��)�}(c��ng)��(k��)�Ď�(k��)�����(���w���ǰ���ռ���g���Բ�Ӌ(j��))

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�^(gu��)�c(di��n)A(0��1)��б�ʞ�k��ֱ��l�c�AC��(x��2)2��(y��3)2��1����M��N���c(di��n)��
(1)��k��ȡֵ������
(2)��![]() ��12������O������(bi��o)ԭ�c(di��n)����|MN|.
��12������O������(bi��o)ԭ�c(di��n)����|MN|.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪ȫ����R���O(sh��)����A={x|��x+2����x-5����0}��![]() ��C={x|a+1��x��2a-1}��
��C={x|a+1��x��2a-1}��
��1����A��B����CRA����B��
��2����C��A��B������(sh��)��(sh��)a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij��Ʒ��һ��(g��)��(n��i)��30�죩�A(y��)Ӌ(j��)���N��![]() �������c�r(sh��)�gt(��)���P(gu��n)ϵ��D1��ʾ���r(ji��)
�������c�r(sh��)�gt(��)���P(gu��n)ϵ��D1��ʾ���r(ji��)![]() ���f(w��n)Ԫ/�����c�r(sh��)�gt(��)�ĺ���(sh��)�P(gu��n)ϵ��D2��ʾ����t������(sh��)��
���f(w��n)Ԫ/�����c�r(sh��)�gt(��)�ĺ���(sh��)�P(gu��n)ϵ��D2��ʾ����t������(sh��)��
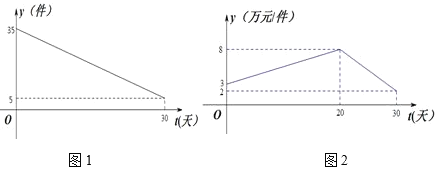
��1��ԇ��(xi��)��![]() �c
�c![]() �Ľ���ʽ��
�Ľ���ʽ��
��2�������Ʒ���N���~�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����������![]() �У�
�� ![]() ��
�� ![]() ���c(di��n)
���c(di��n)![]() ��
�� ![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ��
��
��![]() �����C��
�����C�� ![]() ƽ��
ƽ��![]() ��
��
��![]() ����������
����������![]() ���w�e��
���w�e��
��![]() ������
������![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() �������ڣ�ָ���c(di��n)
�������ڣ�ָ���c(di��n)![]() ��λ�ò��C�����������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��λ�ò��C�����������ڣ�Ո(q��ng)�f(shu��)�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M��12�֣�
��֪���タC�ķ���C��y2="2" p x��p��0���^(gu��)�c(di��n)A��1��-2��.
��I�����タC�ķ��̣��������(zh��n)�����̣�
��II���Ƿ����ƽ����OA��O������(bi��o)ԭ�c(di��n)����ֱ��l��ʹ��ֱ��l�c���タC�й����c(di��n)����ֱ��OA�cl�ľ��x����![]() �������ڣ����ֱ��l�ķ��̣��������ڣ��f(shu��)�����ɡ�
�������ڣ����ֱ��l�ķ��̣��������ڣ��f(shu��)�����ɡ�
���𰸡���I�����タC�ķ��̞�![]() �����(zh��n)�����̞�
�����(zh��n)�����̞�![]() ��II�������}���ֱ��l ���ڣ��䷽�̞�2x+y-1 =0.
��II�������}���ֱ��l ���ڣ��䷽�̞�2x+y-1 =0.
��������
ԇ�}���������タ��(bi��o)��(zh��n)���̣�һ�����ô���ϵ��(sh��)����ֻ��һ��(g��)��(d��)���l���_��p��ֵ������2��2��2p��1������p��2�����ɒ��タ���̴_�����(zh��n)�����̣�![]() �����������}���O(sh��)
�����������}���O(sh��)![]() ��
��![]() ������ֱ��OA�c
������ֱ��OA�c![]() �ľ��x����
�ľ��x����![]() ����(j��)�ɗlƽ�о����x��ʽ�ã�
����(j��)�ɗlƽ�о����x��ʽ�ã�![]() ���
���![]() ���ٸ���(j��)ֱ��
���ٸ���(j��)ֱ��![]() �c���タC�й����c(di��n)�_��
�c���タC�й����c(di��n)�_��![]()
ԇ�}�������� ��1������1����2������y2��2px���ã���2��2��2p��1��
����p��2��
������Ē��タC�ķ��̞�![]()
���(zh��n)�����̞�![]() ��
��
��2�����O(sh��)���ڷ����}���ֱ��![]() ��
��
�䷽�̞�![]() ��
��
��![]() ��
��![]() ��
��
��?y��n)�ֱ��![]() �c���タC�й����c(di��n)��
�c���タC�й����c(di��n)��
��������4��8t��0�����![]() ��
��
��һ���棬��ֱ��OA��![]() �ľ��x
�ľ��x![]()
�ɵ�![]() �����
�����![]() ��
��
��?y��n)�?/span>1[��![]() ����������1��[��
����������1��[��![]() ����������
����������
���Է����}���ֱ��![]() ���ڣ��䷽�̞�
���ڣ��䷽�̞�![]() ��
��
���c(di��n)�����タ���̣�ֱ���c���タλ���P(gu��n)ϵ
�������c(di��n)�������タ�Ę�(bi��o)��(zh��n)���̵ķ���������
��1�����������タ�Ę�(bi��o)��(zh��n)���̳��ô���ϵ��(sh��)������?y��n)�δ֪�?sh��)ֻ��p������ֻ��һ��(g��)�l���_��pֵ���ɣ�
��2�����̣���?y��n)钁�タ�������ķN��(bi��o)��(zh��n)��ʽ��������タ���̕r(sh��)�����ȶ�λ���ٶ�����
���ѣ����(bi��o)��(zh��n)����Ҫ�ȴ_����ʽ����Ҫ�r(sh��)Ҫ�M(j��n)�з��ӑՓ����(bi��o)��(zh��n)�����Еr(sh��)���O(sh��)��y2=mx��x2=my��m��0����
���}�͡�����}
���Y(ji��)����
22
���}Ŀ����֪�E�A![]() ��
��![]() �����ҽ��c(di��n)�c����S��һ��(g��)���c(di��n)���������ε�����(g��)��c(di��n)���c(di��n)
�����ҽ��c(di��n)�c����S��һ��(g��)���c(di��n)���������ε�����(g��)��c(di��n)���c(di��n)![]() �ڙE�A
�ڙE�A![]() ��.
��.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() �^(gu��)�E�A���c(di��n)
�^(gu��)�E�A���c(di��n)![]() ���E�A��
���E�A��![]() ��
��![]() ��E�A���S������c(di��n)����(d��ng)ֱ��
��E�A���S������c(di��n)����(d��ng)ֱ��![]() �r(sh��)����
�r(sh��)����![]() ����e.
����e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ��(g��)�������b��9��(g��)��������4��(g��)�t��3��(g��)�S���2��(g��)�G���@Щ����ɫ����ȫ��ͬ
![]() �ĺ������S�C(j��)ȡ��2��(g��)����ȡ����2��(g��)���ɫ��ͬ�ĸ���.
�ĺ������S�C(j��)ȡ��2��(g��)����ȡ����2��(g��)���ɫ��ͬ�ĸ���.
![]() �ĺ������S�C(j��)ȡ��4��(g��)�����мt��(g��)��(sh��)�քeӛ��X�����S�C(j��)׃��X�ķֲ��к͔�(sh��)�W(xu��)����.
�ĺ������S�C(j��)ȡ��4��(g��)�����мt��(g��)��(sh��)�քeӛ��X�����S�C(j��)׃��X�ķֲ��к͔�(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com