
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,傾斜角為
,傾斜角為![]() 的直線
的直線![]() 經過橢圓
經過橢圓![]() 的右焦點且與圓
的右焦點且與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,且交橢圓
,且交橢圓![]() 于
于![]() 兩點,射線
兩點,射線![]() 于橢圓
于橢圓![]() 交于點
交于點![]() ,設
,設![]() 的面積于
的面積于![]() 的面積分別為
的面積分別為![]() .
.
①求![]() 的最大值;
的最大值;
②當![]() 取得最大值時,求
取得最大值時,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)根據離心率為![]() 、圓心到直線距離等于半徑,結合性質
、圓心到直線距離等于半徑,結合性質![]() ,列出關于
,列出關于![]() 、
、![]() 、
、![]() 的方程組,求出
的方程組,求出![]() 、
、![]() 、
、![]() ,即可得橢圓
,即可得橢圓![]() 的方程;(2) 直線
的方程;(2) 直線![]() 與圓
與圓![]() 相切得:
相切得: 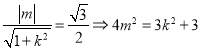 ,將直線
,將直線![]() 代入橢圓
代入橢圓![]() 的方程得:
的方程得: ![]() ①根據點到直線距離公式、弦長公式結合韋達定理及三角形面積公式可得
①根據點到直線距離公式、弦長公式結合韋達定理及三角形面積公式可得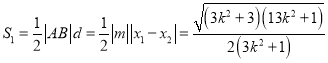 ,利用基本不等式可得結果;②當
,利用基本不等式可得結果;②當![]() 取得最大值時,
取得最大值時, ![]() ,
,  .
.
試題解析:(1)依題直線![]() 的斜率
的斜率![]() .設直線
.設直線![]() 的方程為
的方程為![]() ,
,
依題有: 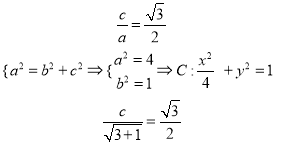
(2)由直線![]() 與圓
與圓![]() 相切得:
相切得: 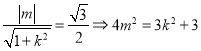 .
.
設![]() .將直線
.將直線![]() 代入橢圓
代入橢圓![]() 的方程得:
的方程得: ![]()
![]() ,且
,且![]() .
.![]()
設點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,故
,故![]() 的面積為:
的面積為:
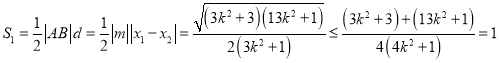 ,
,
當![]() .等號成立.故
.等號成立.故![]() 的最大值為1.
的最大值為1.
設![]() ,由直線
,由直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,可得
,可得![]() ,
,
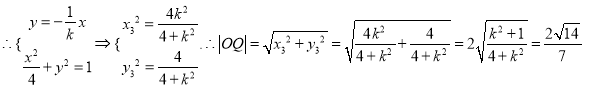 .
.
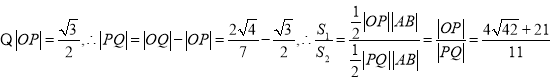 .,
.,
【方法點晴】本題主要考查待定系數法求橢圓方程及圓錐曲線求最值,屬于難題.解決圓錐曲線中的最值問題一般有兩種方法:一是幾何意義,特別是用圓錐曲線的定義和平面幾何的有關結論來解決,非常巧妙;二是將圓錐曲線中最值問題轉化為函數問題,然后根據函數的特征選用參數法、配方法、判別式法、三角函數有界法、函數單調性法以及均值不等式法,本題(2)就是用的這種思路,利用均值不等式法求三角形面積最值的.


科目:高中數學 來源: 題型:
【題目】某校為保證學生夜晚安全,實行教師值夜班制度,已知![]() 共5名教師每周一到周五都要值一次夜班,每周如此,且沒有兩人同時值夜班,周六和周日不值夜班,若
共5名教師每周一到周五都要值一次夜班,每周如此,且沒有兩人同時值夜班,周六和周日不值夜班,若![]() 昨天值夜班,從今天起
昨天值夜班,從今天起![]() 至少連續4天不值夜班,
至少連續4天不值夜班, ![]() 周四值夜班,則今天是周___________.
周四值夜班,則今天是周___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=x-(a+1)ln x-![]() (a∈R),g (x)=
(a∈R),g (x)=![]() x2+ex-xex.
x2+ex-xex.
(1)當x∈[1,e] 時,求f (x)的最小值;
(2)當a<1時,若存在x1∈[e,e2],使得對任意的x2∈[-2,0],f (x1)<g (x2)恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校或班級舉行活動,通常需要張貼海報進行宣傳.現讓你設計一張如圖所示的豎向張貼的海報,要求版心面積為128 dm2,上、下兩邊各空2 dm,左、右兩邊各空1 dm.如何設計海報的尺寸,才能使四周空白面積最小?
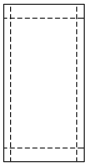
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() (其中
(其中![]() ).
).
(1)若點![]() 的直角坐標為
的直角坐標為![]() ,且點
,且點![]() 在曲線
在曲線![]() 內,求實數
內,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,當
,當![]() 變化時,求直線
變化時,求直線![]() 被曲線
被曲線![]() 截得的弦長的取值范圍.
截得的弦長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)若函數![]() 在區間
在區間![]() 上是單調函數,試求實數
上是單調函數,試求實數![]() 的取值范圍;
的取值范圍;
(2)已知函數![]() ,且
,且![]() ,若函數
,若函數![]() 在區間
在區間![]() 上恰有3個零點,求實數
上恰有3個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分15分)如圖,在半徑為![]() 的半圓形(O為圓心)鐵皮上截取一塊矩形材料ABCD,其中點A、B在直徑上,點C、D在圓周上,將所截得的矩形鐵皮ABCD卷成一個以AD為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),記圓柱形罐子的體積為
的半圓形(O為圓心)鐵皮上截取一塊矩形材料ABCD,其中點A、B在直徑上,點C、D在圓周上,將所截得的矩形鐵皮ABCD卷成一個以AD為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),記圓柱形罐子的體積為![]()
![]() .
.
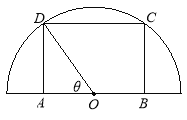
(1)按下列要求建立函數關系式:
①設![]() ,將
,將![]() 表示為
表示為![]() 的函數;
的函數;
②設![]() (
(![]() ),將
),將![]() 表示為
表示為![]() 的函數;
的函數;
(2)請您選用(1)問中的一個函數關系,求圓柱形罐子的最大體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com