Question

已知直線y＝mx與函數的圖象恰好有3個不同的公共點，則實數m的取值范圍是（   ）

A．(，4)

B．(，＋∞)

C．(，5)

D．(，)

Answer 1

B

作出函數的圖象，如圖所示．

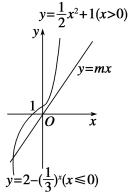
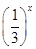
直線y＝mx的圖象是繞坐標原點旋轉的動直線．當斜率m≤0時，直線y＝mx與函數f(x)的圖象只有一個公共點；當m>0時，直線y＝mx始終與函數y＝2－(x≤0)的圖象有一個公共點，故要使直線y＝
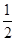
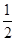
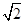
mx與函數f(x)的圖象有三個公共點，必須使直線y＝mx與函數y＝x²＋1 (x>0)的圖象有兩個公共點，即方程mx＝x²＋1在x>0時有兩個不相等的實數根，即方程x²－2mx＋2＝0的判別式Δ＝4m²－4×2>0，解得m>.故所求實數m的取值范圍是(，＋∞).
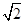