
【題目】已知橢圓![]() :
:![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點相同,
的焦點相同,![]() ,
,![]() 為橢圓的左、右焦點.
為橢圓的左、右焦點.![]() 為橢圓上任意一點,△
為橢圓上任意一點,△![]() 面積的最大值為1.
面積的最大值為1.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() :
:![]()
![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點.
兩點.
(i)若直線![]() 與
與![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,且
,且![]() ,求證:直線
,求證:直線![]() 過定點,并求出該定點的坐標;
過定點,并求出該定點的坐標;
(ii)若直線![]() 的斜率時直線
的斜率時直線![]() ,
,![]() 斜率的等比中項,求△
斜率的等比中項,求△![]() 面積的取值范圍.
面積的取值范圍.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)
(ii)![]()
【解析】
試題分析:(1)先根據拋物線![]() 的焦點
的焦點![]() 得
得![]() ,再結合橢圓幾何條件得當點
,再結合橢圓幾何條件得當點![]() 為橢圓的短軸端點時,△
為橢圓的短軸端點時,△![]() 面積最大,此時
面積最大,此時![]() ,所以
,所以![]() .(2)(i)證明直線過定點問題,一般方法以算代證,即求出直線方程,根據方程特征確定其過定點,本題關鍵求出
.(2)(i)證明直線過定點問題,一般方法以算代證,即求出直線方程,根據方程特征確定其過定點,本題關鍵求出![]() 之間關系即可得出直線過定點.由
之間關系即可得出直線過定點.由![]() 得
得![]() ,即
,即![]() ,因此聯立直線與橢圓方程,結合韋達定理可得;(ii)先分析條件:直線
,因此聯立直線與橢圓方程,結合韋達定理可得;(ii)先分析條件:直線![]() 的斜率時直線
的斜率時直線![]() ,
,![]() 斜率的等比中項,即
斜率的等比中項,即![]() ,
,![]() ,化簡得
,化簡得![]() ,聯立直線與橢圓方程,結合韋達定理可得
,聯立直線與橢圓方程,結合韋達定理可得![]() ,這樣三角形面積可用m表示,其中高利用點到直線距離得到,底邊邊長利用弦長公式得到:
,這樣三角形面積可用m表示,其中高利用點到直線距離得到,底邊邊長利用弦長公式得到:![]() ,最后根據基本不等式求最值
,最后根據基本不等式求最值
試題解析:(1)由拋物線的方程![]() 得其焦點為
得其焦點為![]() ,所以橢圓中
,所以橢圓中![]() ,
,
當點![]() 為橢圓的短軸端點時,△
為橢圓的短軸端點時,△![]() 面積最大,此時
面積最大,此時![]() ,所以
,所以![]() .
.
![]() ,
,![]() 為橢圓的左、右焦點,
為橢圓的左、右焦點,![]() 為橢圓上任意一點,△
為橢圓上任意一點,△![]() 面積的最大值為1,
面積的最大值為1,
所以橢圓的方程為![]() .
.
(2)聯立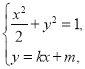 得
得![]() ,
,
![]() ,得
,得![]() (*)
(*)
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
(i)![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]() ,
,
得![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,因此直線
,因此直線![]() 恒過定點,該定點坐標為
恒過定點,該定點坐標為![]() .
.
(ii)因為直線![]() 的斜率是直線
的斜率是直線![]() ,
,![]() 斜率的等比中項,所以
斜率的等比中項,所以![]() ,即
,即![]() ,
,
得![]() ,得
,得![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
代入(*),得![]() .
.
![]() .
.
設點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則![]() ,
,
所以![]()
![]()
![]() ,
,
當且僅當![]() ,即
,即![]() 時,△
時,△![]() 面積取最大值
面積取最大值![]() .
.
故△![]() 面積的取值范圍為
面積的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】50.6,0.65,log0.55的大小順序是( )
A.0.65 < log0.65 < 50.6B.0.65 < 50.6< log0.65
C.log0.65 < 50.6 <0.65D.log0.65 <0.65 < 50.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用數學歸納法證明當n∈N*時,1+2+22+…+25n-1是31的倍數時,當n=1時原式為( )
A. 1 B. 1+2
C. 1+2+3+4 D. 1+2+22+23+24
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于給定的兩個變量的統計數據,下列說法正確的是__________.(填序號)
①都可以分析出兩個變量的關系;
②都可以用一條直線近似地表示兩者的關系;
③都可以作出散點圖;
④都可以用確定的表達式表示兩者的關系。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車公司為了考查某![]() 店的服務態度,對到店維修保養的客戶進行回訪調查,每個用戶在到此店或保養后可以對該店進行打分,最高分為10分.上個月公司對該
店的服務態度,對到店維修保養的客戶進行回訪調查,每個用戶在到此店或保養后可以對該店進行打分,最高分為10分.上個月公司對該![]() 店的100位到店維修保養的客戶進行了調查,將打分的客戶按所打分值分成以下幾組:第一組
店的100位到店維修保養的客戶進行了調查,將打分的客戶按所打分值分成以下幾組:第一組![]() ,第二組
,第二組![]() ,第三組
,第三組![]() ,第四組
,第四組![]() a,第五組
a,第五組![]() ,得到頻率分布直方圖如圖所示.
,得到頻率分布直方圖如圖所示.
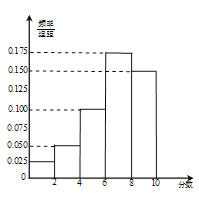
(1)求所打分值在![]() 的客戶的人數;
的客戶的人數;
(2)該公司在第二、三組客戶中按分層抽樣的方法抽取6名客戶進行深入調查,之后將從這6人中隨機抽取2人進行物質獎勵,求得到獎勵的人來自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小李參加一種紅包接龍游戲:他在紅包里塞了12元,然后發給朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 將獲得紅包里的所有金額;如果
將獲得紅包里的所有金額;如果![]() 未猜中,
未猜中,![]() 將當前的紅包轉發給朋友
將當前的紅包轉發給朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 平分紅包里的金額;如果
平分紅包里的金額;如果![]() 未猜中,
未猜中,![]() 將當前的紅包轉發給朋友
將當前的紅包轉發給朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 和
和![]() 平分紅包里的金額;如果
平分紅包里的金額;如果![]() 未猜中,紅包里的錢將退回小李的賬戶,設
未猜中,紅包里的錢將退回小李的賬戶,設![]() 猜中的概率分別為
猜中的概率分別為![]() ,且
,且![]() 是否猜中互不影響.
是否猜中互不影響.
(1)求![]() 恰好獲得4元的概率;
恰好獲得4元的概率;
(2)設![]() 獲得的金額為
獲得的金額為![]() 元,求
元,求![]() 的分布列;
的分布列;
(3)設![]() 獲得的金額為
獲得的金額為![]() 元,
元,![]() 獲得的金額為
獲得的金額為![]() 元,判斷
元,判斷![]() 所獲得的金額的期望能否超過
所獲得的金額的期望能否超過![]() 的期望與
的期望與![]() 的期望之和.
的期望之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是 ( )
A. 任何兩個變量都具有相關關系
B. 人的知識與其年齡具有相關關系
C. 散點圖中的各點是分散的沒有規律
D. 根據散點圖求得的回歸直線方程都是有意義的
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com