【題目】如圖，扇形的半徑為r cm，周長為20cm，問扇形的圓心角α等于多少弧度時，這個扇形的面積最大，并求出扇形面積的最大值．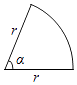 
【答案】解：設扇形的半徑為r，弧長為l，則：l+2r=20，即l=20﹣2r（0＜r＜10）． 扇形的面積S= 
lr，將上式代入，得：S= （20﹣2r）r=﹣r2+10r=﹣（r﹣5）2+25，
所以：當且僅當r=5時，S有最大值25，
此時：l=20﹣2×5=10，α= 
=2rad．
所以：當α=2rad時，扇形的面積取最大值，最大值為25cm2
【解析】設扇形的半徑為r，弧長為l，利用周長關系，表示出扇形的面積，利用二次函數求出面積的最大值，以及圓心角的大小．
【考點精析】本題主要考查了扇形面積公式的相關知識點，需要掌握若扇形的圓心角為
，半徑為
，弧長為
，周長為
，面積為
，則
，
，
才能正確解答此題．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】身穿紅、黃兩種顏色衣服的各有兩人，身穿藍顏色衣服的有一人，現將這五人排成一行，要求穿相同顏色衣服的人不能相鄰，則不同的排法共有（ ）
A. 24種 B. 28種 C. 36種 D. 48種
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出以下說法：①不共面的四點中，任意三點不共線；
②有三個不同公共點的兩個平面重合；
③沒有公共點的兩條直線是異面直線；
④分別和兩條異面直線都相交的兩條直線異面；
⑤一條直線和兩條異面直線都相交，則它們可以確定兩個平面．
其中正確結論的序號是_______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{xn}滿足x1=1，x2=λ，并且 
=λ 
（λ為非零常數，n=2，3，4，…）． （Ⅰ）若x1 ， x3 ， x5成等比數列，求λ的值；
（Ⅱ）設0＜λ＜1，常數k∈N* ， 證明 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據下列條件求雙曲線的標準方程：
(1)經過點(
，3)，且一條漸近線方程為4x＋3y＝0.
(2)P(0,6)與兩個焦點的連線互相垂直，與兩個頂點連線的夾角為
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2015高考山東文數】某中學調查了某班全部
名同學參加書法社團和演講社團的情況，數據如下表：（單位：人）
參加書法社團 | 未參加書法社團 | |
參加演講社團 |
|
|
未參加演講社團 |
|
|
（1）從該班隨機選
名同學，求該同學至少參加上述一個社團的概率；
（2）在既參加書法社團又參加演講社團的
名同學中，有5名男同學
名女同學
現從這
名男同學和名女同學中各隨機選
人，求
被選中且
未被選中的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
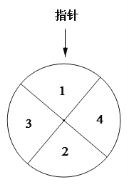
【題目】【2016高考山東文數】某兒童樂園在“六一”兒童節推出了一項趣味活動.參加活動的兒童需轉動如圖所示的轉盤兩次，每次轉動后，待轉盤停止轉動時，記錄指針所指區域中的數.設兩次記錄的數分別為x，y.獎勵規則如下：
①若
，則獎勵玩具一個；
②若
，則獎勵水杯一個； ③其余情況獎勵飲料一瓶.
假設轉盤質地均勻，四個區域劃分均勻.小亮準備參加此項活動.
（I）求小亮獲得玩具的概率；
（II）請比較小亮獲得水杯與獲得飲料的概率的大小，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線
的極坐標方程為
，直線
的參數方程為
（
為參數， 
）.
（Ⅰ）把曲線
的極坐標方程化為直角坐標方程，并說明曲線
的形狀；
（Ⅱ）若直線
經過點
，求直線
被曲線
截得的線段
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
