【題目】（本題滿分12分）
一個盒子中裝有4張卡片，每張卡片上寫有1個數字，數字分別是1、2、3、4，現從盒子中隨機抽取卡片.
(Ⅰ)若一次從中隨機抽取3張卡片，求3張卡片上數字之和大于或等于7的概率；
(Ⅱ)若第一次隨機抽取1張卡片，放回后再隨機抽取1張卡片，求兩次抽取的卡片中至少一次抽到數字2的概率.
【答案】（1）
（2）
【解析】
古典概型要求能夠列舉出所有事件和發生事件的個數，本題可以列舉出所有事件，概率問題同其他的知識點結合在一起，實際上是以概率問題為載體，主要考查的是另一個知識點
（1）由題意知本題是一個古典概型，試驗包含的所有事件是任取三張卡片，三張卡片上的數字全部可能的結果，可以列舉出，而滿足條件的事件數字之和大于7的，可以從列舉出的結果中看出．
（2）列舉出每次抽1張，連續抽取兩張全部可能的基本結果，而滿足條件的事件是兩次抽取中至少一次抽到數字3，從前面列舉出的結果中找出來．
解：(Ⅰ)設A表示事件“抽取3張卡片上的數字之和大于或等于7”，任取三張卡片，三張卡片上的數字全部可能的結果是（1、2、3），（1、2、4），（1、3、4），（2、3、4），共4種，……………………………2分
數字之和大于或等于7的是（1、2、4），（1、3、4），（2、3、4），共3種，……4分
所以P(A)=. ……………6分
(Ⅱ)設B表示事件“至少一次抽到2”，
第一次抽1張，放回后再抽取1張的全部可能結果為：（1、1）（1、2）（1、3）（1、4）（2、1）（2、2）（2、3）（2、4）（3、1）（3、2）（3、3）（3、4）（4、1）（4、2）（4、3）（4、4），共16個 ……………………………8分
事件B包含的結果有（1、2）（2、1）（2、2）（2、3）（2、4）（3、2）（4、2），共7個
………10分
所以所求事件的概率為P(B)=. ……………12分
課時訓練江蘇人民出版社系列答案科目：高中數學 來源： 題型：
【題目】直三棱柱ABC﹣A1B1C1的底面是等腰直角三角形，AB=AC=2，四棱錐C﹣ABB1A1的體積等于4． 
（1）求AA1的值；
（2）求C1到平面A1B1C的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】己知函數f（x）=xlnx．
（1）求曲線f（x）在點（1，f（1））處的切線方程；
（2）對x≥1，f（x）≤m（x2﹣1）成立，求實數m的最小值；
（3）證明：1n 
．（n∈N*）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位共有老、中、青職工430人,其中青年職工160人，中年職工人數是老年職工人數的2倍。為了解職工身體狀況，現采用分層抽樣方法進行調查，在抽取的樣本中有青年職工32人，則該樣本中的老年職工人數為
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為棱長
的正方體， 
為棱
的中點.
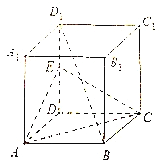
（1）求三棱錐
的體積；
（2）求證： 
平面
.
【答案】（1）
;（2）見解析.
【解析】試題分析：（1）高為ED,再根據錐體體積公式計算體積（2）連接
交
于點
，根據三角形中位線性質得
，再根據線面平行判定定理得結論
試題解析：（1）體積
（2）連接
交
于點
，則
為
的中位線，即
，
又
面
， 
面
，得到
平面
.
【題型】解答題
【結束】
18
【題目】已知拋物線
： 
的焦點
為圓
的圓心.
（1）求拋物線
的標準方程；
（2）若斜率
的直線
過拋物線的焦點
與拋物線相交于
兩點，求弦長
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}滿足a1=1，nan+1=（n+1）an+n（n+1），n∈N* ．
（1）證明：數列{ 
}是等差數列；
（2）設bn=3n 
，求數列{bn}的前n項和Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知以坐標原點
為圓心的圓與拋物線
相交于不同的兩點
， 
，與拋物線
的準線相交于不同的兩點
， 
，且
.
(1)求拋物線
的方程；
(2)若不經過坐標原點
的直線
與拋物線
相交于不同的兩點
， 
，且滿足
.證明直線
過定點
，并求出點
的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分10分）已知等差數列{an}滿足a1＋a2＝10，a4－a3＝2.
(1)求{an}的通項公式．
(2)設等比數列{bn}滿足b2＝a3，b3＝a7.問：b6與數列{an}的第幾項相等？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
