【題目】已知橢圓
的左，右焦點分別
,過
的直線l交橢圓于A,B兩點，若
的最大值為5，則b的值為（ ）
A. 1 B. 
C. 
D. 
【答案】C
【解析】
由題意可知橢圓是焦點在x軸上的橢圓，利用橢圓定義得到|BF2|+|AF2|＝8﹣|AB|，再由過橢圓焦點的弦中通徑的長最短，可知當AB垂直于x軸時|AB|最小，把|AB|的最小值b2代入|BF2|+|AF2|＝8﹣|AB|，由|BF2|+|AF2|的最大值等于5列式求b的值．
由0＜b＜2可知，焦點在x軸上，∴a=2,
∵過F1的直線l交橢圓于A，B兩點，∴|BF2|+|AF2|+|BF1|+|AF1|＝2a+2a＝4a＝8
∴|BF2|+|AF2|＝8﹣|AB|．
當AB垂直x軸時|AB|最小，|BF2|+|AF2|值最大，
此時|AB|＝b2，∴5＝8﹣b2，
解得
．
故選
．
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系中，曲線
的參數方程是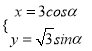
（
為參數）以原點為極點， 
軸正半軸為極軸，并取與直角坐標系相同的單位長度，建立極坐標系，曲線
的極坐標方程是
.
（1）求曲線
， 
的直角坐標方程；
（2）若
、
分別是曲線
和
上的任意點，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某住宅小區為了使居民有一個優雅舒適的生活環境，計劃建一個八邊形的休閑小區，它的主體造型的平面圖是由兩個相同的矩形ABCD和EFGH構成的面積為200平方米的十字型地域．現計劃在正方形MNPQ上建花壇，造價為4200元/平方米，在四個相同的矩形上（圖中陰影部分）鋪花崗巖地坪，造價為210元/平方米，再在四個空角上鋪草坪，造價為80元/平方米．
（1）設總造價為S元，AD的邊長為x米，DQ的邊長為y米，試建立S關于x的函數關系式；
（2）計劃至少要投入多少元，才能建造這個休閑小區．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設等差數列
的前
項和為
，數列
的前項和為
，下列說法錯誤的是（ ）
A. 若有最大值，則也有最大值
B. 若有最大值，則也有最大值
C. 若數列
不單調，則數列
也不單調
D. 若數列不單調，則數列也不單調
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在高為6的等腰梯形
中， 
，且
， 
，將它沿對稱軸
折起，使平面
平面
.如圖2，點
為
中點，點
在線段
上（不同于
， 
兩點），連接
并延長至點
，使
.
（1）證明： 
平面
；
（2）若
，求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業為打入國際市場，決定從
兩種產品中只選擇一種進行投資生產.已知投資生產這兩種產品的有關數據如下表：（單位：萬美元）
其中年固定成本與年生產的件數無關，
為待定常數，其值由生產
產品的原材料價格決定，預計
.另外，年銷售
件
產品時需上交
萬美元的特別關稅.假設生產出來的產品都能在當年銷售出去.
（1）寫出該廠分別投資生產兩種產品的年利潤
與生產相應產品的件數之間的函數關系，并指明其定義域；
（2）如何投資才可獲得最大年利潤？請你做出規劃.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知奇函數f（x）=（a-x）|x|，常數a∈R，且關于x的不等式mx2+m＞f[f（x）]對所有的x∈[-2，2]恒成立，則實數m的取值范圍是______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點P到定點
的距離比它到直線
的距離小2，設動點P的軌跡為曲線C．
求曲線C的方程；
若直線
與曲線C和圓
從左至右的交點依次為A，B，C，D求
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
