
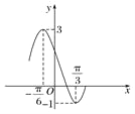
【題目】已知函數(shù)g(x)=Acos(ωx+φ)+B的部分圖象如圖所示,將函數(shù)g(x)的圖象保持縱坐標(biāo)不變,橫坐標(biāo)向右平移![]() 個(gè)單位長(zhǎng)度后得到函數(shù)f(x)的圖象.求:
個(gè)單位長(zhǎng)度后得到函數(shù)f(x)的圖象.求:
(1)函數(shù)f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范圍.
【答案】(1) [0,3] (2)![]()
【解析】
(1)由函數(shù)的圖象的頂點(diǎn)坐標(biāo)求出A,由周期求出ω,由五點(diǎn)法作圖求出φ的值,可得函數(shù)g(x)的解析式.再根據(jù)函數(shù)y=Acos(ωx+φ)+B的圖象的平移變換規(guī)律,可得f(x)的解析式,再根據(jù)x∈[![]() ,
,![]() ],利用余弦函數(shù)的定義域和值域求得可得f(x)的值域;
],利用余弦函數(shù)的定義域和值域求得可得f(x)的值域;
(2)由f(x)≥2可得 cos(2x![]() )
)![]() ,故有2kπ
,故有2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈z,由此求得不等式的解集.
,k∈z,由此求得不等式的解集.
(1)由圖知B=![]() =1,A=
=1,A=![]() =2,T=2(
=2,T=2(![]() )=π,
)=π,
所以ω=2,所以g(x)=2cos(2x+φ)+1.
把(![]() )代入,得2cos(
)代入,得2cos(![]() )+1=-1,
)+1=-1,
即![]() +φ=π+2kπ(k∈Z),
+φ=π+2kπ(k∈Z),
所以φ=2kπ+![]() (k∈Z).
(k∈Z).
因?yàn)閨φ|<![]() ,所以φ=
,所以φ=![]() ,
,
所以g(x)=2cos(2x+![]() )+1,
)+1,
所以f(x)=2cos(2x-![]() )+1.
)+1.
因?yàn)?/span>x∈![]() ,所以2x-
,所以2x-![]() ∈
∈![]() ,
,
所以f(x)∈[0,3],即函數(shù)f(x)在![]() 上的值域?yàn)閇0,3].
上的值域?yàn)閇0,3].
(2)因?yàn)?/span>f(x)=2cos(2x-![]() )+1,
)+1,
所以2cos(2x-![]() )+1≥2,
)+1≥2,
所以cos(2x-![]() )≥
)≥![]() ,
,
所以-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2kπ(k∈Z),
+2kπ(k∈Z),
所以kπ≤x≤kπ+![]() (k∈Z),
(k∈Z),
所以使f(x)≥2成立的x的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】正方體![]() 的棱長(zhǎng)為1,
的棱長(zhǎng)為1,![]() 分別為
分別為![]() 的中點(diǎn).則( )
的中點(diǎn).則( )

A.直線![]() 與直線
與直線![]() 垂直B.直線
垂直B.直線![]() 與平面
與平面![]() 平行
平行
C.平面![]() 截正方體所得的截面面積為
截正方體所得的截面面積為![]() D.點(diǎn)
D.點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 到平面
到平面![]() 的距離相等
的距離相等
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 時(shí),對(duì)任意的
時(shí),對(duì)任意的![]() 都成立,求實(shí)數(shù)
都成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)求關(guān)于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() .
.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時(shí),記
時(shí),記![]() 的最小值為
的最小值為![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
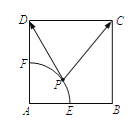
【題目】如圖,已知正方形![]() 的邊長(zhǎng)為2,點(diǎn)
的邊長(zhǎng)為2,點(diǎn)![]() 為
為![]() 的中點(diǎn).以
的中點(diǎn).以![]() 為圓心,
為圓心,![]() 為半徑,作弧交
為半徑,作弧交![]() 于點(diǎn)
于點(diǎn)![]() .若
.若![]() 為劣弧
為劣弧![]() 上的動(dòng)點(diǎn),則
上的動(dòng)點(diǎn),則![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】輪船在海上航行時(shí),需要借助無(wú)線電導(dǎo)航確認(rèn)自己所在的位置,以把握航向.現(xiàn)有![]() 、
、![]() 、
、![]() 三個(gè)無(wú)線電發(fā)射臺(tái),其中
三個(gè)無(wú)線電發(fā)射臺(tái),其中![]() 在陸地上,
在陸地上,![]() 在海上,
在海上,![]() 在某國(guó)海岸線上,(該國(guó)這段海岸線可以近似地看作直線的一部分),如下圖.已知
在某國(guó)海岸線上,(該國(guó)這段海岸線可以近似地看作直線的一部分),如下圖.已知![]() 、
、![]() 兩點(diǎn)距離10千米,
兩點(diǎn)距離10千米,![]() 是
是![]() 的中點(diǎn),海岸線與直線
的中點(diǎn),海岸線與直線![]() 的夾角為
的夾角為![]() .為保證安全,輪船的航路始終要滿足:接收到
.為保證安全,輪船的航路始終要滿足:接收到![]() 點(diǎn)的信號(hào)比接收到
點(diǎn)的信號(hào)比接收到![]() 點(diǎn)的信號(hào)晚
點(diǎn)的信號(hào)晚![]() 秒.(注:無(wú)線電信號(hào)每秒傳播
秒.(注:無(wú)線電信號(hào)每秒傳播![]() 千米).在某時(shí)刻,測(cè)得輪船距離
千米).在某時(shí)刻,測(cè)得輪船距離![]() 點(diǎn)距離為4千米.
點(diǎn)距離為4千米.

(1)以點(diǎn)![]() 為原點(diǎn),直線
為原點(diǎn),直線![]() 為
為![]() 軸建立平面直角坐標(biāo)系(如圖),求出該時(shí)刻輪船的位置;
軸建立平面直角坐標(biāo)系(如圖),求出該時(shí)刻輪船的位置;
(2)根據(jù)經(jīng)驗(yàn),船只在距離海岸線1.5千米以內(nèi)的海域航行時(shí),有擱淺的風(fēng)險(xiǎn).如果輪船保持目前的航路不變,那么是否有擱淺風(fēng)險(xiǎn)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖為一個(gè)正方體![]() 與一個(gè)半球
與一個(gè)半球![]() 構(gòu)成的組合體,半球
構(gòu)成的組合體,半球![]() 的底面圓與該正方體的上底面
的底面圓與該正方體的上底面![]() 的四邊相切,
的四邊相切, ![]() 與正方形
與正方形![]() 的中心重合.將此組合體重新置于一個(gè)球
的中心重合.將此組合體重新置于一個(gè)球![]() 中(球
中(球![]() 未畫出),使該正方體的下底面
未畫出),使該正方體的下底面![]() 的頂點(diǎn)均落在球
的頂點(diǎn)均落在球![]() 的表面上,半球
的表面上,半球![]() 與球
與球![]() 內(nèi)切,設(shè)切點(diǎn)為
內(nèi)切,設(shè)切點(diǎn)為![]() ,若正四棱錐
,若正四棱錐![]() 的表面積為
的表面積為![]() ,則球
,則球![]() 的表面積為( )
的表面積為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】同時(shí)拋擲1角、5角和1元的三枚硬幣,計(jì)算:
(1)恰有一枚出現(xiàn)正面的概率;
(2)至少有兩枚出現(xiàn)正面的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ln x-![]() .
.
(1)試討論f(x)在定義域上的單調(diào)性;
(2)若f(x)在[1,e]上的最小值為![]() ,求a的值.
,求a的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com